A floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
1. 12MgR
2. 78MgR
3. 58MgR
4. 34MgR
The correct Answer is:B
To solve the problem, we need to calculate the decrease in potential energy when a floor mat of mass M is unrolled from a cylinder of radius R to a cylinder of radius R2.
1. Calculate Initial Potential Energy (PE_initial):
- When the mat is rolled into a cylinder of radius R, the center of mass of the mat is at a height R from the ground.
- The potential energy of the entire mat can be calculated using the formula:
PEinitial=M⋅g⋅R
2. Determine the Mass Distribution:
- When the mat is unrolled to a radius of R2, some part of the mat will be lying flat on the ground.
- The mass distribution is uniform, so we need to find the mass that remains in the cylinder of radius R2.
- The area of the original cylinder is πR2 and the area of the new cylinder is π(R2)2=πR24.
- The mass of the unrolled part (lying flat) can be calculated as:
Mass of unrolled part=M−M4=3M4
- Therefore, the mass of the mat that remains in the cylinder is:
Mremaining=M4
3. Calculate Final Potential Energy (PE_final):
- The center of mass of the remaining mass in the cylinder of radius R2 is at a height of R2.
- The potential energy of the remaining mass can be calculated as:
PEfinal=(M4)⋅g⋅(R2)=M⋅g⋅R8
4. Calculate the Decrease in Potential Energy (ΔPE):
- The decrease in potential energy is given by:
ΔPE=PEinitial−PEfinal
- Substituting the values we calculated:
ΔPE=(M⋅g⋅R)−(M⋅g⋅R8)
- Simplifying this:
ΔPE=M⋅g⋅R(1−18)=M⋅g⋅R⋅78
Thus, the decrease in potential energy is:
ΔPE=7M⋅g⋅R8
- When the mat is rolled into a cylinder of radius R, the center of mass of the mat is at a height R from the ground.
- The potential energy of the entire mat can be calculated using the formula:
PEinitial=M⋅g⋅R
- When the mat is unrolled to a radius of R2, some part of the mat will be lying flat on the ground.
- The mass distribution is uniform, so we need to find the mass that remains in the cylinder of radius R2.
- The area of the original cylinder is πR2 and the area of the new cylinder is π(R2)2=πR24.
- The mass of the unrolled part (lying flat) can be calculated as:
Mass of unrolled part=M−M4=3M4
- Therefore, the mass of the mat that remains in the cylinder is:
Mremaining=M4
- The center of mass of the remaining mass in the cylinder of radius R2 is at a height of R2.
- The potential energy of the remaining mass can be calculated as:
PEfinal=(M4)⋅g⋅(R2)=M⋅g⋅R8
- The decrease in potential energy is given by:
ΔPE=PEinitial−PEfinal
- Substituting the values we calculated:
ΔPE=(M⋅g⋅R)−(M⋅g⋅R8)
- Simplifying this:
ΔPE=M⋅g⋅R(1−18)=M⋅g⋅R⋅78
ΔPE=7M⋅g⋅R8
Topper's Solved these Questions
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png) View Solution
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


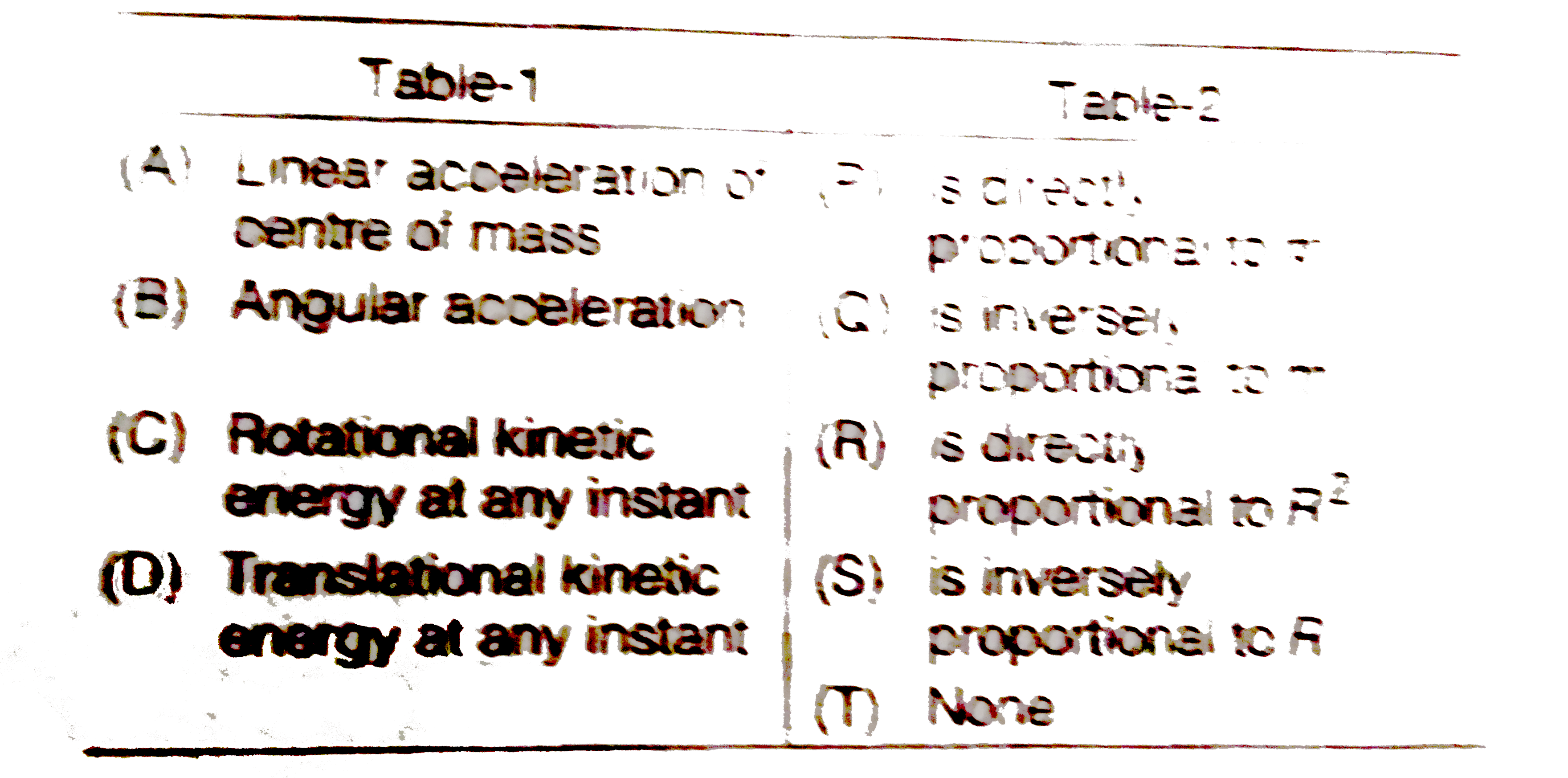 View Solution
View SolutionA body of mass m taken form the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be
View SolutionA body of mass m taken form the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA rectangular sheat of paper 44cm x 18cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View Solution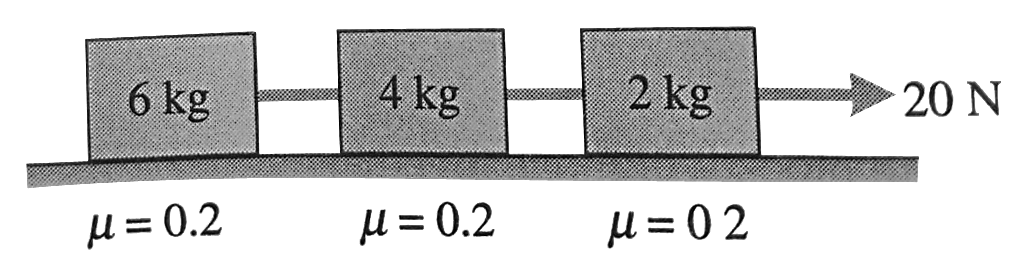
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses isView SolutionA rectangular sheet of paper 44cmAND18cm is a rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
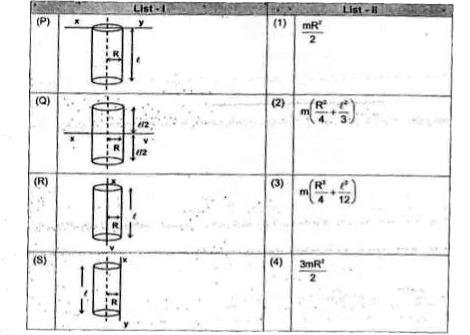 View Solution
View Solution

