Resistances P, Q, S and R are arranged in a cyclic order to form a balanced Wheatstone's network. The ratio of power consumed in the branches (P+Q) and (R+S) is
1:1
R:P
P2:Q2
P2:R2
The correct Answer is:B
To solve the problem regarding the ratio of power consumed in the branches of a balanced Wheatstone network, we can follow these steps:
Step 1: Understand the Wheatstone Bridge Configuration
In a balanced Wheatstone bridge, we have four resistances P, Q, R, and S arranged in a cyclic order. The branches of the bridge are (P + Q) and (R + S).
Step 2: Write the Expression for Power
The power consumed in any branch can be expressed using the formula:
P=V2R
where V is the potential difference across the branch and R is the equivalent resistance of that branch.
Step 3: Identify the Branches
For the two branches:
- The first branch (P + Q) has a power P1:
P1=V2P+Q
- The second branch (R + S) has a power P2:
P2=V2R+S
Step 4: Calculate the Ratio of Powers
The ratio of the powers consumed in the two branches can be expressed as:
P1P2=V2P+QV2R+S
This simplifies to:
P1P2=R+SP+Q
Step 5: Use the Condition of a Balanced Bridge
In a balanced Wheatstone bridge, the condition is:
PR=QS
From this, we can derive:
PQ=RS
Let’s denote this ratio as K.
Step 6: Express the Resistors in Terms of K
Using the ratio K:
- We can express S in terms of R and K:
S=RK
- Similarly, express Q in terms of P:
Q=PK
Step 7: Substitute Back into the Power Ratio
Now substitute S and Q back into the power ratio:
P1P2=R+RKP+PK
This can be simplified:
P1P2=R(1+1K)P(1+1K)
The (1+1K) terms cancel out:
P1P2=RP
Conclusion
Thus, the final ratio of power consumed in the branches (P + Q) and (R + S) is:
P1P2=RP
In a balanced Wheatstone bridge, we have four resistances P, Q, R, and S arranged in a cyclic order. The branches of the bridge are (P + Q) and (R + S).
The power consumed in any branch can be expressed using the formula:
P=V2R
where V is the potential difference across the branch and R is the equivalent resistance of that branch.
For the two branches:
- The first branch (P + Q) has a power P1:
P1=V2P+Q
- The second branch (R + S) has a power P2:
P2=V2R+S
The ratio of the powers consumed in the two branches can be expressed as:
P1P2=V2P+QV2R+S
This simplifies to:
P1P2=R+SP+Q
In a balanced Wheatstone bridge, the condition is:
PR=QS
From this, we can derive:
PQ=RS
Let’s denote this ratio as K.
Using the ratio K:
- We can express S in terms of R and K:
S=RK
- Similarly, express Q in terms of P:
Q=PK
Now substitute S and Q back into the power ratio:
P1P2=R+RKP+PK
This can be simplified:
P1P2=R(1+1K)P(1+1K)
The (1+1K) terms cancel out:
P1P2=RP
Thus, the final ratio of power consumed in the branches (P + Q) and (R + S) is:
P1P2=RP
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - METER BRIDGE
4 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - POTENTIOMETER
7 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - KIRCHOFF S LAW
14 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
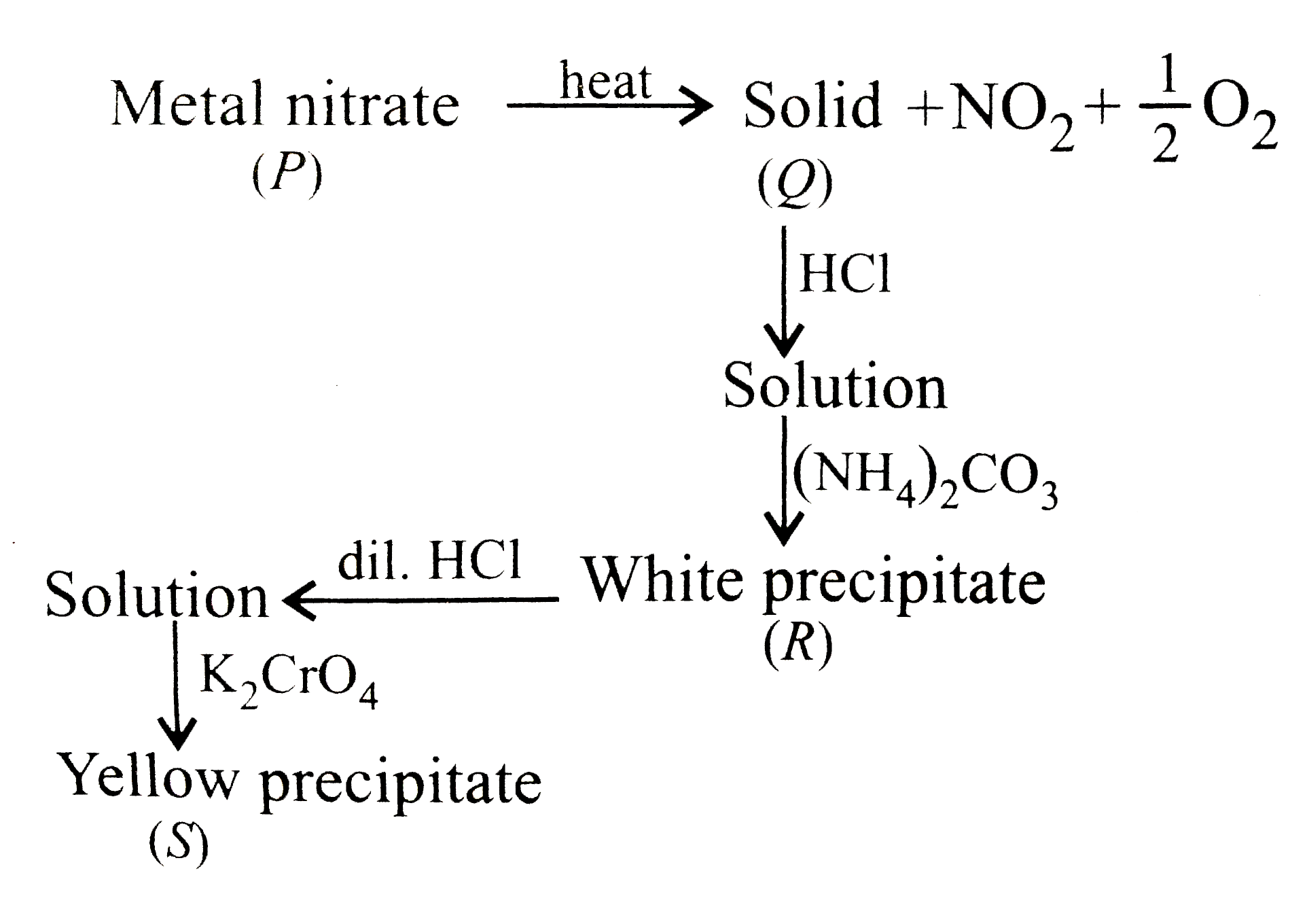
What are (P),(Q),(R) and (S)?
View SolutionIn a balanced wheatstone's network, the resistances in the arms Q and S are interchanged. As result of this:
View SolutionIdentity P,Q,R and S in the diagram

View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionIn a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)
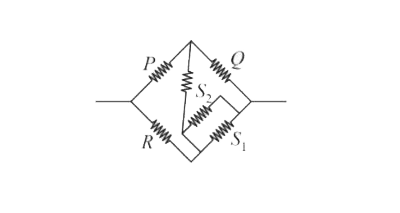
View SolutionIn a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)

View SolutionIn two similar triangles ABC and PQR , if their corresponding altitudes AD and PS are in the ratio 4:9, find the ratio of the areas of triangle ABC and triangle PQR .
View SolutionIn a Wheatstone bridge (see fige ) Resitances P and Q are approximately equal .When R=400Ω the bridge is blanced .on is inerchanging P and Q ,the value of R, for balance is 405 Ω .The value of X is close to :

View SolutionIn a Wheatstone's bridge, three resistances P,Q and R connected in the three arms and the fourth arm is formed by two resistances S1andS2 connected in parallel. The condition for the bridge to be balanced will be
View Solution
