Four resistances of respectively are used to form a Wheatstone bridge. The resistance is short circuited with a resistance R in order to get bridge balanced. The value of R will be
The correct Answer is:C
To solve the problem of finding the resistance R that balances the Wheatstone bridge, we can follow these steps:
Step 1: Understand the Wheatstone Bridge Configuration
In a Wheatstone bridge, we have four resistances arranged in a diamond shape. Here, we have three resistances of 3Ω each and one resistance of 4Ω. The 4Ω resistance is short-circuited with an unknown resistance R.
Step 2: Identify the Resistors
Let:
- R1=3Ω
- R2=3Ω
- R3=3Ω
- R4=4Ω (which is short-circuited with R)
Step 3: Calculate the Equivalent Resistance of R4
When the 4Ω resistor is short-circuited with R, the equivalent resistance Req of R4 can be calculated using the formula for resistors in parallel:
Req=R⋅4R+4
Step 4: Set Up the Balance Condition
For the Wheatstone bridge to be balanced, the following condition must hold:
R1R2=ReqR3
Substituting the known values:
33=Req3
This simplifies to:
1=Req3
Step 5: Solve for Req
From the balance condition, we can express Req:
Req=3Ω
Step 6: Substitute Req into the Equivalent Resistance Formula
Now we can substitute Req back into the equivalent resistance formula:
3=R⋅4R+4
Step 7: Cross-Multiply and Solve for R
Cross-multiplying gives:
3(R+4)=4R
Expanding this:
3R+12=4R
Rearranging gives:
12=4R−3R
Thus:
R=12Ω
Final Answer
The value of the resistance R that balances the Wheatstone bridge is:
12Ω
In a Wheatstone bridge, we have four resistances arranged in a diamond shape. Here, we have three resistances of 3Ω each and one resistance of 4Ω. The 4Ω resistance is short-circuited with an unknown resistance R.
Let:
- R1=3Ω
- R2=3Ω
- R3=3Ω
- R4=4Ω (which is short-circuited with R)
When the 4Ω resistor is short-circuited with R, the equivalent resistance Req of R4 can be calculated using the formula for resistors in parallel:
Req=R⋅4R+4
For the Wheatstone bridge to be balanced, the following condition must hold:
R1R2=ReqR3
Substituting the known values:
33=Req3
This simplifies to:
1=Req3
From the balance condition, we can express Req:
Req=3Ω
Now we can substitute Req back into the equivalent resistance formula:
3=R⋅4R+4
Cross-multiplying gives:
3(R+4)=4R
Expanding this:
3R+12=4R
Rearranging gives:
12=4R−3R
Thus:
R=12Ω
The value of the resistance R that balances the Wheatstone bridge is:
12Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - METER BRIDGE
4 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - POTENTIOMETER
7 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - KIRCHOFF S LAW
14 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Current in 3Ω resistance is

View SolutionFour resistence of 10Ω,60Ω,100Ωand 200Ω, respectively taken in order are used to form a Wheatstone's bridge . A 15 V battery is connected to the ends of a 200Ωresistance, the current through it will be
View SolutionIn Wheatstone bridge, four resistors of resistances 15Ω,12Ω,4Ω and 10Ω respectively, are connected in cyclic order. The resistance ( in Ω) that is to be connected in parallel with the resistance of 10Ω to balance the network is
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
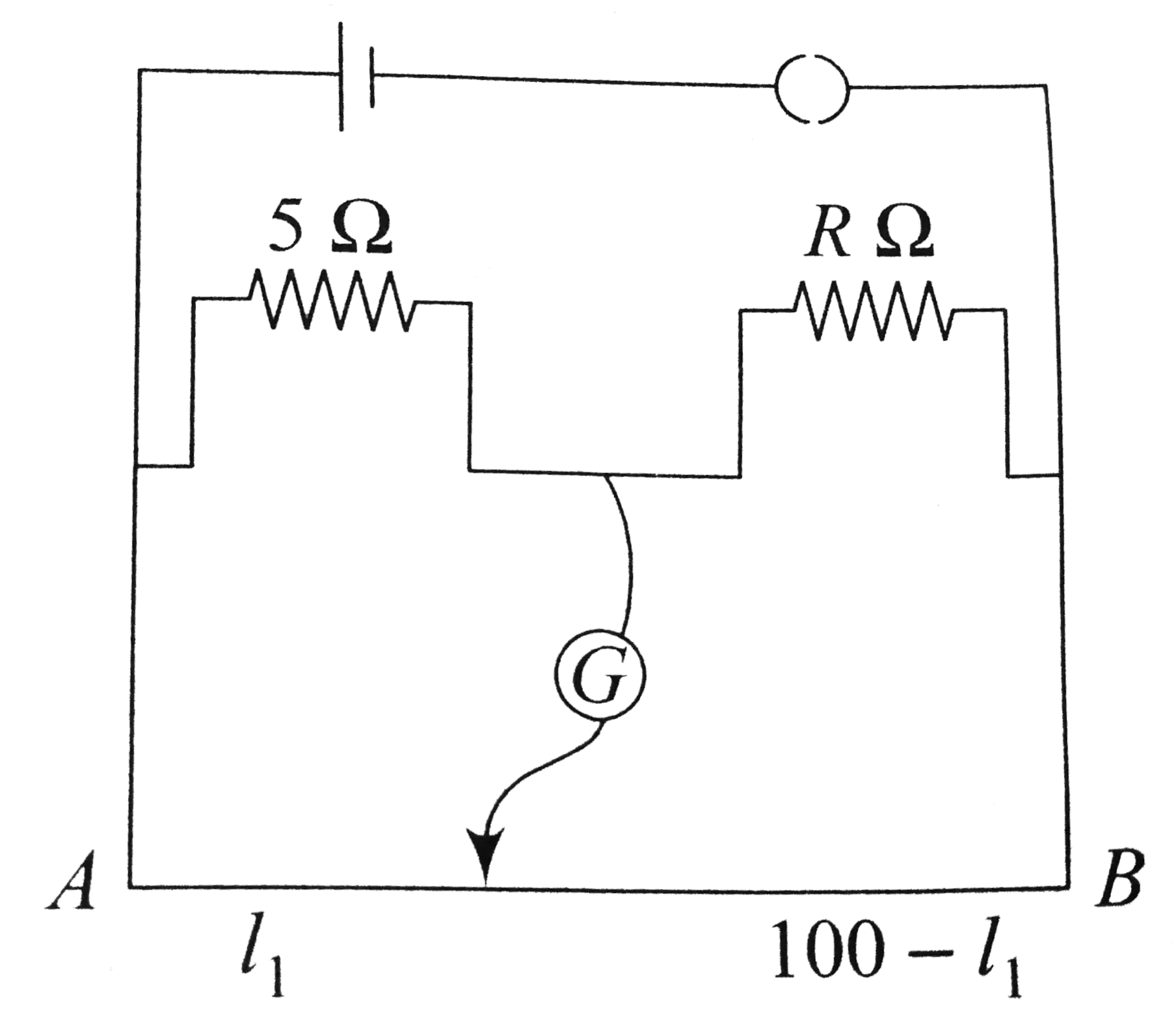
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is

View SolutionThree resistance of values 2Ω,3Ω and 6Ω are to be connected to produce an effective resistance of 4Ω. This can be done by connecting.
View SolutionFour resistors A, and D form a Wheatstone bridge.
The bridge is balanced , when C = 100Ω If A and B are interchanged the bridge balances for C=121Ω. The value of D is
View SolutionIn the circuit shown, the current in 3Ω resistance is

View Solution
