Point out the best representation of relation between magnetic susceptibility (Chi) and temperature (T) for a paramagnetic material
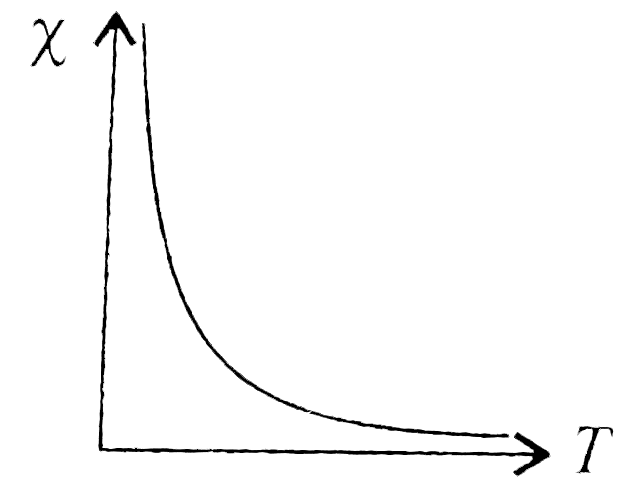
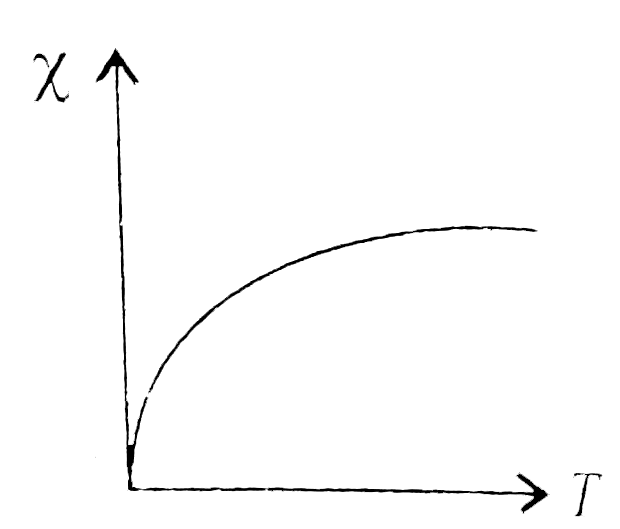
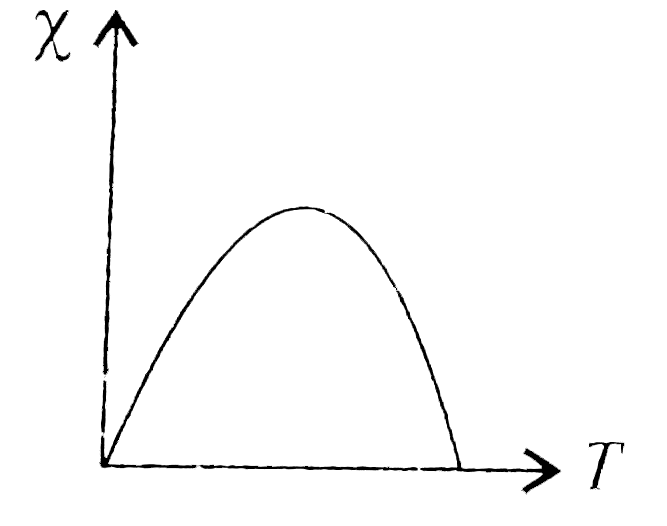
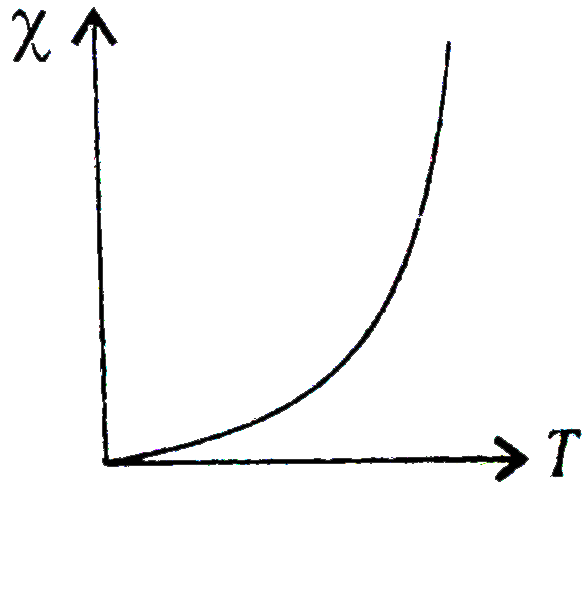
The correct Answer is:A
To determine the best representation of the relationship between magnetic susceptibility (χ) and temperature (T) for a paramagnetic material, we can follow these steps:
1. Understand the Concept of Magnetic Susceptibility:
- Magnetic susceptibility (χ) is a measure of how much a material will become magnetized in an applied magnetic field. For paramagnetic materials, this susceptibility varies with temperature.
2. Recall Curie's Law:
- According to Curie's Law, the magnetic susceptibility (χ) of a paramagnetic material is inversely proportional to its absolute temperature (T). This relationship can be expressed mathematically as:
χ=CT
where C is Curie's constant.
3. Analyze the Inverse Relationship:
- From the equation χ=CT, we can deduce that as the temperature (T) increases, the magnetic susceptibility (χ) decreases. This indicates an inverse relationship between χ and T.
4. Graphical Representation:
- In a graph representing this relationship, the y-axis would typically represent magnetic susceptibility (χ), and the x-axis would represent temperature (T).
- Since χ decreases as T increases, the graph should slope downwards from left to right.
5. Evaluate Given Graphs:
- Among the provided graphs, we need to identify which one shows a downward trend (decreasing χ with increasing T).
- The correct graph will show that as temperature increases, the value of susceptibility decreases.
6. Select the Correct Option:
- After evaluating the graphs, the first graph (option A) should depict the correct inverse relationship, where χ decreases as T increases.
Conclusion:
The best representation of the relationship between magnetic susceptibility (χ) and temperature (T) for a paramagnetic material is the first graph (option A), which shows a decreasing trend.
- Magnetic susceptibility (χ) is a measure of how much a material will become magnetized in an applied magnetic field. For paramagnetic materials, this susceptibility varies with temperature.
- According to Curie's Law, the magnetic susceptibility (χ) of a paramagnetic material is inversely proportional to its absolute temperature (T). This relationship can be expressed mathematically as:
χ=CT
where C is Curie's constant.
- From the equation χ=CT, we can deduce that as the temperature (T) increases, the magnetic susceptibility (χ) decreases. This indicates an inverse relationship between χ and T.
- In a graph representing this relationship, the y-axis would typically represent magnetic susceptibility (χ), and the x-axis would represent temperature (T).
- Since χ decreases as T increases, the graph should slope downwards from left to right.
- Among the provided graphs, we need to identify which one shows a downward trend (decreasing χ with increasing T).
- The correct graph will show that as temperature increases, the value of susceptibility decreases.
- After evaluating the graphs, the first graph (option A) should depict the correct inverse relationship, where χ decreases as T increases.
The best representation of the relationship between magnetic susceptibility (χ) and temperature (T) for a paramagnetic material is the first graph (option A), which shows a decreasing trend.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - PERMANENT MAGNETS AND ELECTROMAGNETS4videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - HIGHER ORDER THINKING SKILLS (HOTS)8videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - MAGNETISATION AND MAGNETIC INTENSITY11videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason15videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason15videos
MOVING CHARGES AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
The relation connecting magnetic susceptibility χm and relative permeability μr, is
Aχm=μr+1Bχm=μr−1Cχm=1μrDχm=3(1+μr)
The variation of magnetic susceptibility (χ) with temperature for a diamagnetic substance is best represented by
View SolutionThe variation of magnetic susceptibility (χ) with temperature for dimagnetic substance is represented by
View SolutionThe correct graph which shows the variation of paramagnetic susceptibility S with temperature T is
View SolutionMagnetic susceptibility of a paramagnetic substance is
View SolutionIn which type of material the magnetic susceptibility does not depend on temperature?
View SolutionHow does the magnetic susceptibility of a paramagnetic material change with temperature?
View SolutionWhich materials have negative value of magnetic susceptibility?
View Solution