Question

The graph between the angular momentum J and angular velocity $\omega$ will be :-

Options

A.
B.
C.
D.

Answer

A

Explanation

To determine the graph between angular momentum $$J$$ and angular velocity $$\omega$$, we start with the fundamental relationship between these two quantities.

1. Understanding the Relationship:
The angular momentum \( J \) of a rotating object is given by the formula:
\( J = I \omega \)
where \( I \) is the moment of inertia and \( \omega \) is the angular velocity.

2. Identifying the Equation Form:
The equation \( J = I \omega \) can be compared to the standard linear equation form:
\( y = mx + c \)
Here, \( J \) corresponds to \( y \), \( \omega \) corresponds to \( x \), \( I \) is the slope \( m \), and the intercept \( c \) is 0.

3. Analyzing the Intercept:
Since the equation has no constant term (the intercept \( c = 0 \)), the graph will pass through the origin (0,0). This means that when \( \omega = 0 \), \( J \) will also be 0.

4. Determining the Slope:
The slope of the graph is equal to the moment of inertia \( I \). This means that the graph will be a straight line with a slope equal to \( I \).

5. Sketching the Graph:
- The graph will start at the origin (0,0).
- It will be a straight line that increases linearly as \( \omega \) increases.
- The line will have a positive slope, indicating that as angular velocity increases, angular momentum also increases proportionally.

6. Selecting the Correct Graph:
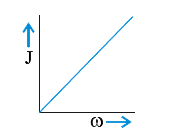
Based on the above analysis, we can conclude that the correct graph will be a straight line passing through the origin with a positive slope.

Conclusion:
The correct option is Option A, which represents the linear relationship between angular momentum \( J \) and angular velocity \( \omega \) with no intercept.