A rope is wound round a hollow cylinder of mass 3kgandradius40cm. If the rope is pulled with a force of 30N, what is the angualr acceleration of the cylinder ?
15rads−2
20rads−2
25rads−2
30rads−2
The correct Answer is:c
To find the angular acceleration of the hollow cylinder when a rope is pulled with a force, we can follow these steps:
Step 1: Identify the given values
- Mass of the hollow cylinder, m=3kg
- Radius of the hollow cylinder, r=40cm=0.4m
- Force applied on the rope, F=30N
Step 2: Calculate the torque (τ)
The torque (τ) exerted on the cylinder due to the force applied on the rope can be calculated using the formula:
τ=r×F
Here, since the force is applied perpendicular to the radius, we can simplify this to:
τ=r⋅F
Substituting the known values:
τ=0.4m×30N=12N m
Step 3: Determine the moment of inertia (I)
The moment of inertia (I) for a hollow cylinder is given by the formula:
I=mr2
Substituting the values:
I=3kg×(0.4m)2=3kg×0.16m2=0.48kg m2
Step 4: Relate torque to angular acceleration (α)
According to the rotational dynamics, the relationship between torque and angular acceleration is given by:
τ=Iα
From this, we can solve for angular acceleration (α):
α=τI
Substituting the values we found:
α=12N m0.48kg m2=25rad/s2
Final Answer
The angular acceleration of the cylinder is:
α=25rad/s2
---
- Mass of the hollow cylinder, m=3kg
- Radius of the hollow cylinder, r=40cm=0.4m
- Force applied on the rope, F=30N
The torque (τ) exerted on the cylinder due to the force applied on the rope can be calculated using the formula:
τ=r×F
Here, since the force is applied perpendicular to the radius, we can simplify this to:
τ=r⋅F
Substituting the known values:
τ=0.4m×30N=12N m
The moment of inertia (I) for a hollow cylinder is given by the formula:
I=mr2
Substituting the values:
I=3kg×(0.4m)2=3kg×0.16m2=0.48kg m2
According to the rotational dynamics, the relationship between torque and angular acceleration is given by:
τ=Iα
From this, we can solve for angular acceleration (α):
α=τI
Substituting the values we found:
α=12N m0.48kg m2=25rad/s2
The angular acceleration of the cylinder is:
α=25rad/s2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ANGULAR MOMENTUM IN CASE OF ROTATIONS ABOUT A FIXED AXIS
16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION
16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - KENEMATICS OF ROTATIONAL MOTION ABOUT A FIXED AXIS
3 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A string is wound around a hollow cylinder of mass 5 Kg and radius 0.5 m. If the string is now pulled with a horizontal force of 40 N, the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string).

View SolutionA rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
View SolutionA rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
View SolutionA rope of negligible mass is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
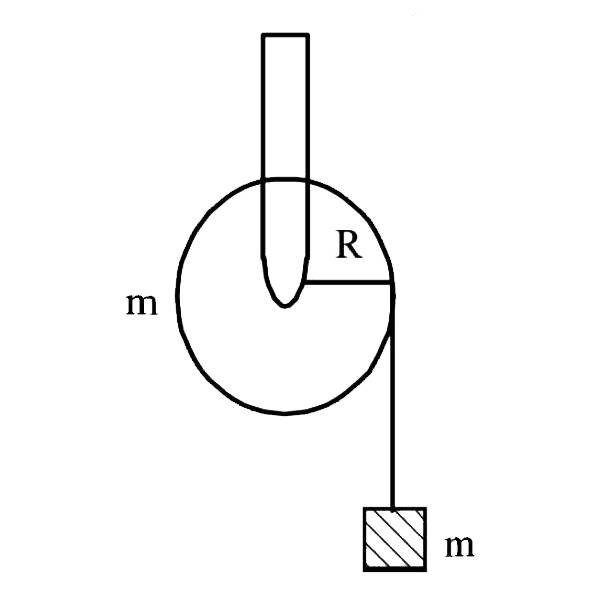
View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
View SolutionA bucket of mass 8 kg is supported by a light rope wound around a solid wooden cylinder of mass 12 kg and radius 20 cm free to rotate about its axis. A man holding the free end of the rope, with the bucket and the cylinder at rest initially, lets go the bucket freely downwards in a well 50 m deep. Neglecting friction, obtain the speed of the bucket and the angular speed of the cylihder just before the bucket enters water.
View SolutionAn angular impulse of 20 Nms is applied to a hollow cylinder of mass 2 kg and radius 20 cm. The change in its angular speed is :
View SolutionA hollow sphere of mass 1 kg and radius 10 cm is free to rotate about its diameter. If a force of 30 N is applied tangentially to it, its angular acceleration is (in rad/s2)
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
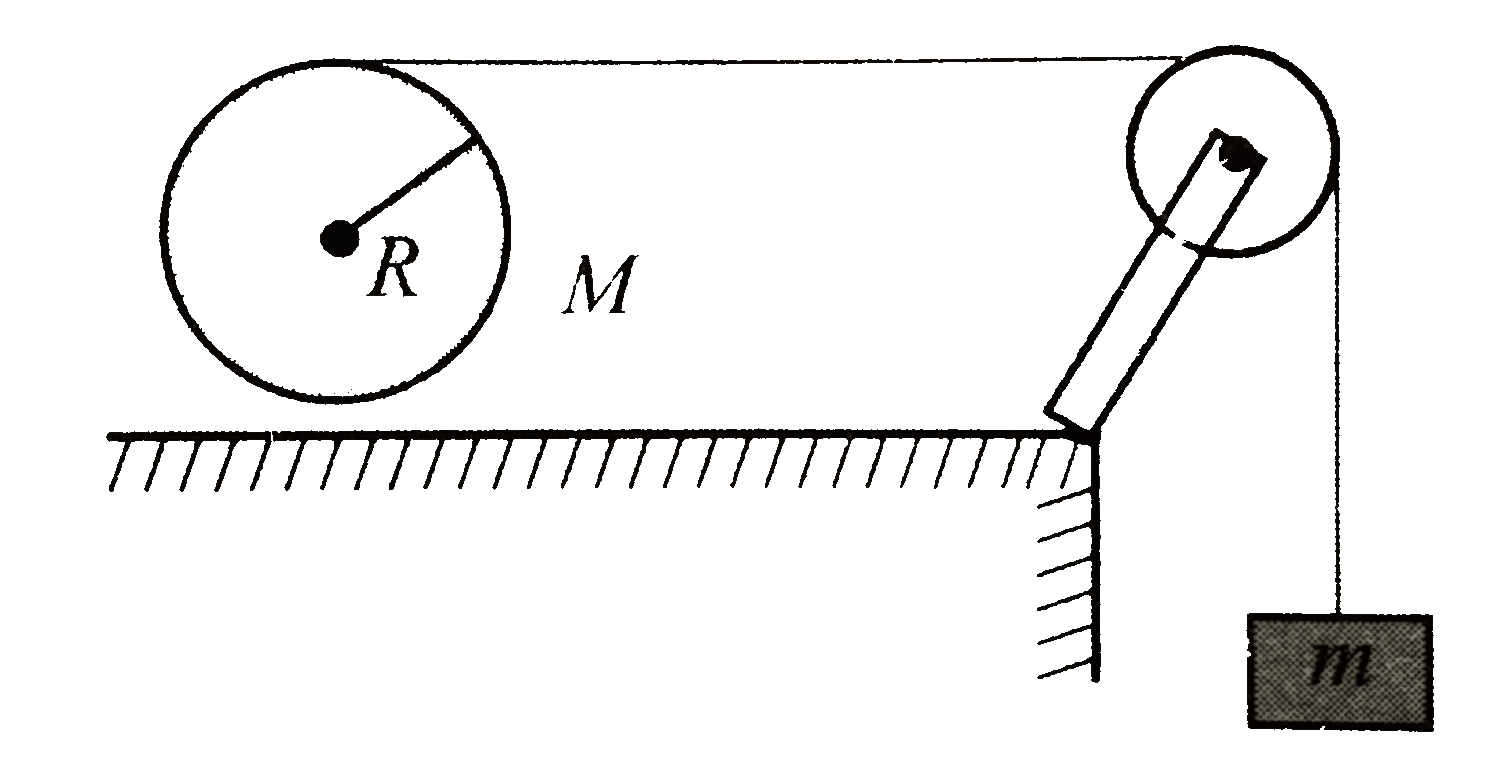
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
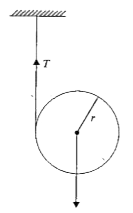
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
View Solution
