A rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
25m/s2
0.25rad/s2
25rad/s2
5m/s2
The correct Answer is:C
To find the angular acceleration of the hollow cylinder when a force is applied to the rope, we can follow these steps:
Step 1: Identify the given values
- Mass of the hollow cylinder, m=3kg
- Radius of the hollow cylinder, r=40cm=0.4m
- Force applied on the rope, F=30N
Step 2: Calculate the torque (τ) applied on the cylinder
The torque is given by the formula:
τ=F×r
Substituting the values:
τ=30N×0.4m=12N m
Step 3: Determine the moment of inertia (I) of the hollow cylinder
For a hollow cylinder, the moment of inertia about its center of mass is given by:
I=m×r2
Substituting the values:
I=3kg×(0.4m)2=3×0.16=0.48kg m2
Step 4: Use the relationship between torque, moment of inertia, and angular acceleration
The relationship is given by:
τ=Iα
Where α is the angular acceleration. Rearranging the formula to solve for α:
α=τI
Substituting the values we calculated:
α=12N m0.48kg m2=25rad/s2
Final Answer
The angular acceleration of the cylinder is:
α=25rad/s2
---
- Mass of the hollow cylinder, m=3kg
- Radius of the hollow cylinder, r=40cm=0.4m
- Force applied on the rope, F=30N
The torque is given by the formula:
τ=F×r
Substituting the values:
τ=30N×0.4m=12N m
For a hollow cylinder, the moment of inertia about its center of mass is given by:
I=m×r2
Substituting the values:
I=3kg×(0.4m)2=3×0.16=0.48kg m2
The relationship is given by:
τ=Iα
Where α is the angular acceleration. Rearranging the formula to solve for α:
α=τI
Substituting the values we calculated:
α=12N m0.48kg m2=25rad/s2
The angular acceleration of the cylinder is:
α=25rad/s2
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)
26 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(JIPMER)
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
A rope of negligible mass is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
View SolutionA string is wound around a hollow cylinder of mass 5 Kg and radius 0.5 m. If the string is now pulled with a horizontal force of 40 N, the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string).

View Solution
Knowledge Check
A rope is wound round a hollow cylinder of mass 3kgandradius40cm. If the rope is pulled with a force of 30N, what is the angualr acceleration of the cylinder ?
A15rads−2B20rads−2C25rads−2D30rads−2
An angular impulse of 20 Nms is applied to a hollow cylinder of mass 2 kg and radius 20 cm. The change in its angular speed is :
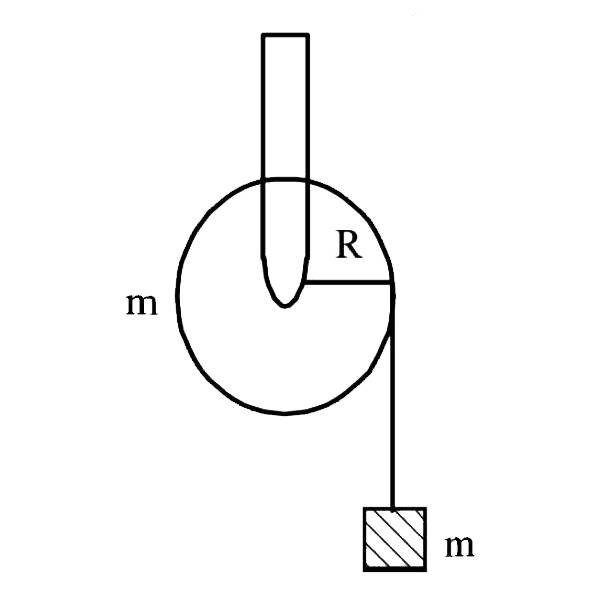
View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
View SolutionA bucket of mass 8 kg is supported by a light rope wound around a solid wooden cylinder of mass 12 kg and radius 20 cm free to rotate about its axis. A man holding the free end of the rope, with the bucket and the cylinder at rest initially, lets go the bucket freely downwards in a well 50 m deep. Neglecting friction, obtain the speed of the bucket and the angular speed of the cylihder just before the bucket enters water.
View SolutionA torque of 10 Nm is applied to a flywheel of mass 10 kg and radius of gyration 50 cm. What is the resultant angular acceleration ?
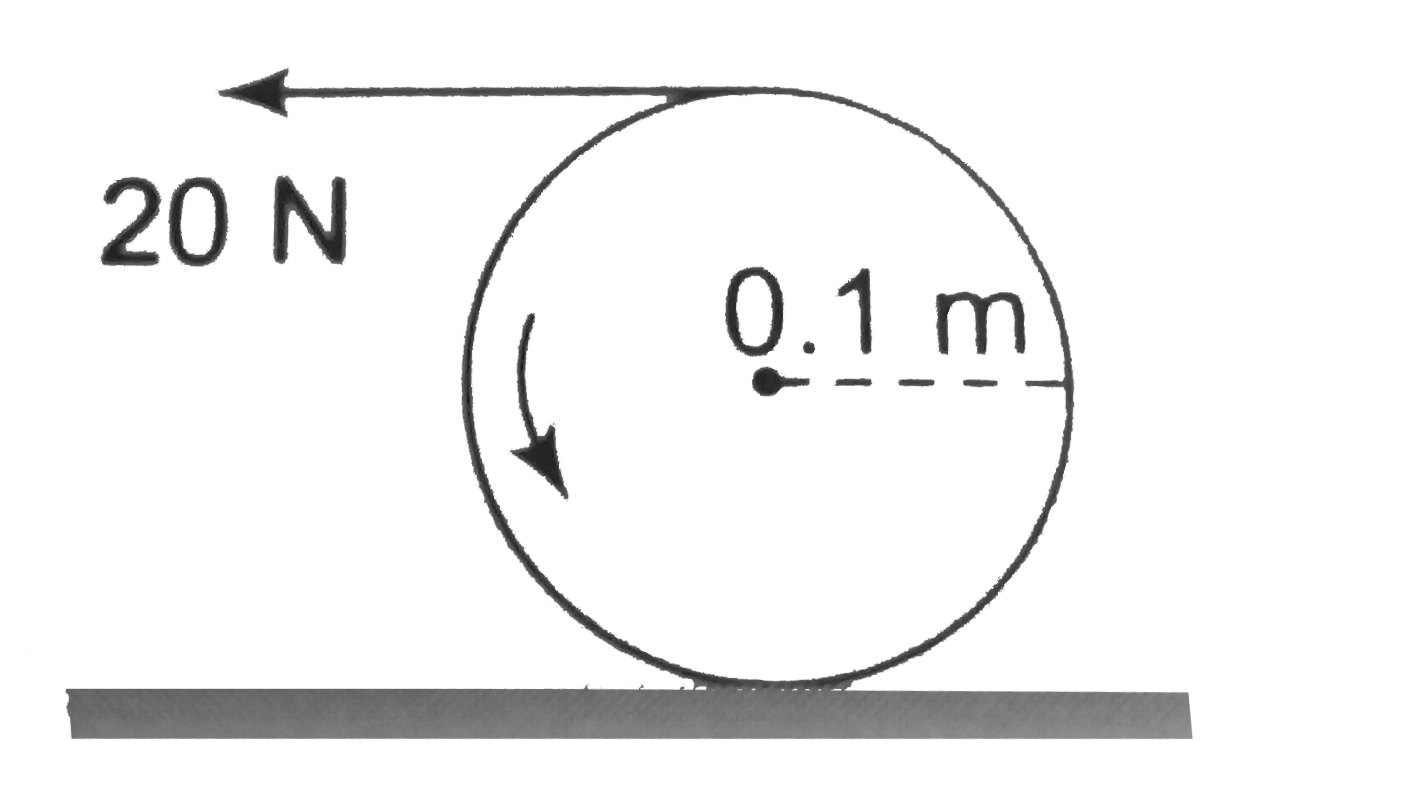
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
 .
.
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionOne end of a massless string is wound around a cylinder of mass 5 kg and radius 16' cm. The cylinder' is mounted symmetrically on a horizontal axle so 5 that It can freely rotate about its axis, to the other end of the string a mass of 500 gm is attached. Calculate the acceleration of the mass when it is released from rest.
View Solution
