A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2 N on the ring and rolls it without slipping with an acceleration of 0.3m/s2. The coeffecient of friction between the ground and the ring is large enough that rolling always occur and the coefficient of friction between the stick and the ring
0.4
0.8
0.2
0.5
The correct Answer is:a
To solve the problem, we will analyze the forces acting on the ring and apply Newton's laws for both translational and rotational motion.
1. Identify the Given Data:
- Mass of the ring, m=2kg
- Radius of the ring, r=0.5m
- Applied force by the stick, F=2N
- Acceleration of the ring, a=0.3m/s2
2. Draw the Free Body Diagram:
- The forces acting on the ring include:
- Weight W=mg acting downwards.
- Normal force N acting upwards.
- Applied force F acting horizontally (to the left).
- Friction force FG acting opposite to the direction of motion (to the right).
- Friction force FS acting at the contact point between the stick and the ring (to the left).
3. Apply Newton's Second Law for Translational Motion:
- The net force in the horizontal direction is given by:
F−FG−FS=ma
- Rearranging gives:
2−FG−FS=2×0.3
- This simplifies to:
2−FG−FS=0.6
- Thus:
FG+FS=1.4(1)
4. Apply Newton's Second Law for Rotational Motion:
- The torque about the center of the ring due to friction forces is:
τ=FG⋅r−FS⋅r=Iα
- The moment of inertia I of a ring is given by I=mr2=2×(0.5)2=0.5kg m2.
- The angular acceleration α can be related to linear acceleration a by α=ar=0.30.5=0.6rad/s2.
- Substituting the values gives:
FG⋅0.5−FS⋅0.5=0.5⋅0.6
- This simplifies to:
FG−FS=0.6(2)
5. Solve the System of Equations:
- We have two equations:
1. FG+FS=1.4
2. FG−FS=0.6
- Adding these two equations:
2FG=2⟹FG=1N
- Substituting FG back into equation (1):
1+FS=1.4⟹FS=0.4N
6. Calculate the Coefficient of Friction:
- The friction force FS is related to the normal force N (which is equal to the applied force since there is no vertical acceleration):
FS=μsN
- Here, N=2N (the applied force).
- Thus:
0.4=μs⋅2
- Solving for μs gives:
μs=0.42=0.2
Final Answer:
The coefficient of friction between the stick and the ring is μs=0.2.
- Mass of the ring, m=2kg
- Radius of the ring, r=0.5m
- Applied force by the stick, F=2N
- Acceleration of the ring, a=0.3m/s2
- The forces acting on the ring include:
- Weight W=mg acting downwards.
- Normal force N acting upwards.
- Applied force F acting horizontally (to the left).
- Friction force FG acting opposite to the direction of motion (to the right).
- Friction force FS acting at the contact point between the stick and the ring (to the left).
- The net force in the horizontal direction is given by:
F−FG−FS=ma
- Rearranging gives:
2−FG−FS=2×0.3
- This simplifies to:
2−FG−FS=0.6
- Thus:
FG+FS=1.4(1)
- The torque about the center of the ring due to friction forces is:
τ=FG⋅r−FS⋅r=Iα
- The moment of inertia I of a ring is given by I=mr2=2×(0.5)2=0.5kg m2.
- The angular acceleration α can be related to linear acceleration a by α=ar=0.30.5=0.6rad/s2.
- Substituting the values gives:
FG⋅0.5−FS⋅0.5=0.5⋅0.6
- This simplifies to:
FG−FS=0.6(2)
- We have two equations:
1. FG+FS=1.4
2. FG−FS=0.6
2FG=2⟹FG=1N
- Substituting FG back into equation (1):
1+FS=1.4⟹FS=0.4N
- The friction force FS is related to the normal force N (which is equal to the applied force since there is no vertical acceleration):
FS=μsN
- Here, N=2N (the applied force).
- Thus:
0.4=μs⋅2
- Solving for μs gives:
μs=0.42=0.2
The coefficient of friction between the stick and the ring is μs=0.2.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - NCER EXAMPLAR PROBLEMS8videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ASSERTION AND REASON15videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION16videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions150videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A boy is pulshing a ring of mass 3 kg and radius 0.6 m with a stick as shown in figure. The stick applies a force of 3N on the ring and rolls it without slipping with an acceleration of 0.4 m/s2
 The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficeient of friction between the stick and the ring is f10 The vlaue of F is View Solution
The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficeient of friction between the stick and the ring is f10 The vlaue of F is View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination '0' then the minimum coefficient of friction required to support pure rolling is
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View Solution
A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isView SolutionA ring of mass m and radius R is acted upon by a force Fas shown in figure. There is sufficient friction between the ring and the ground. The force of friction necessary for pure rolling is
View SolutionA ring of mass m and radius R is acted upon by a force F as shown in the figure. There os sufficient friction between the ring and the ground. The force of friciton force necessary for pure rolling is
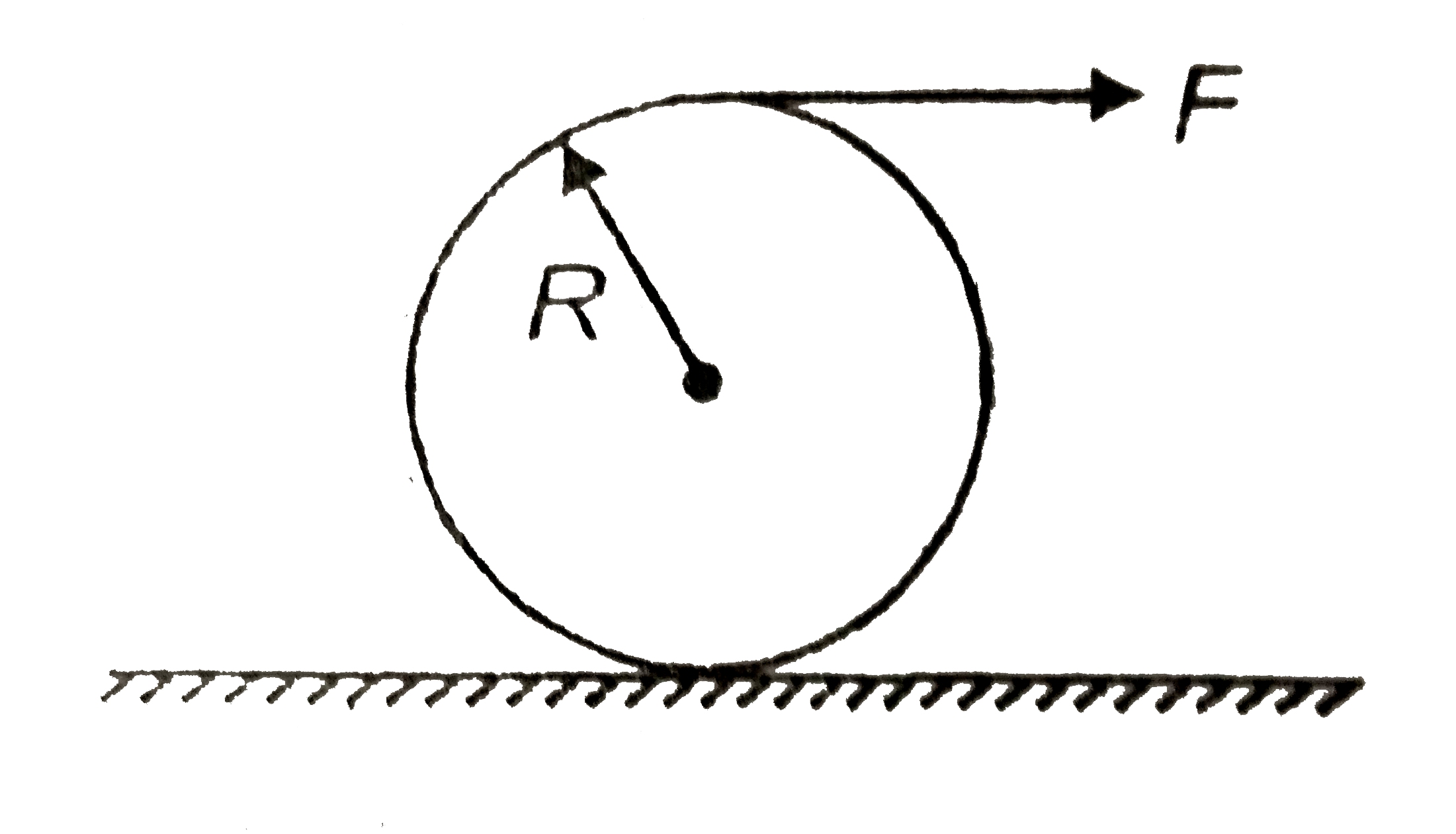 View Solution
View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View SolutionA particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is
 View Solution
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2
 View Solution
View Solution

