Question

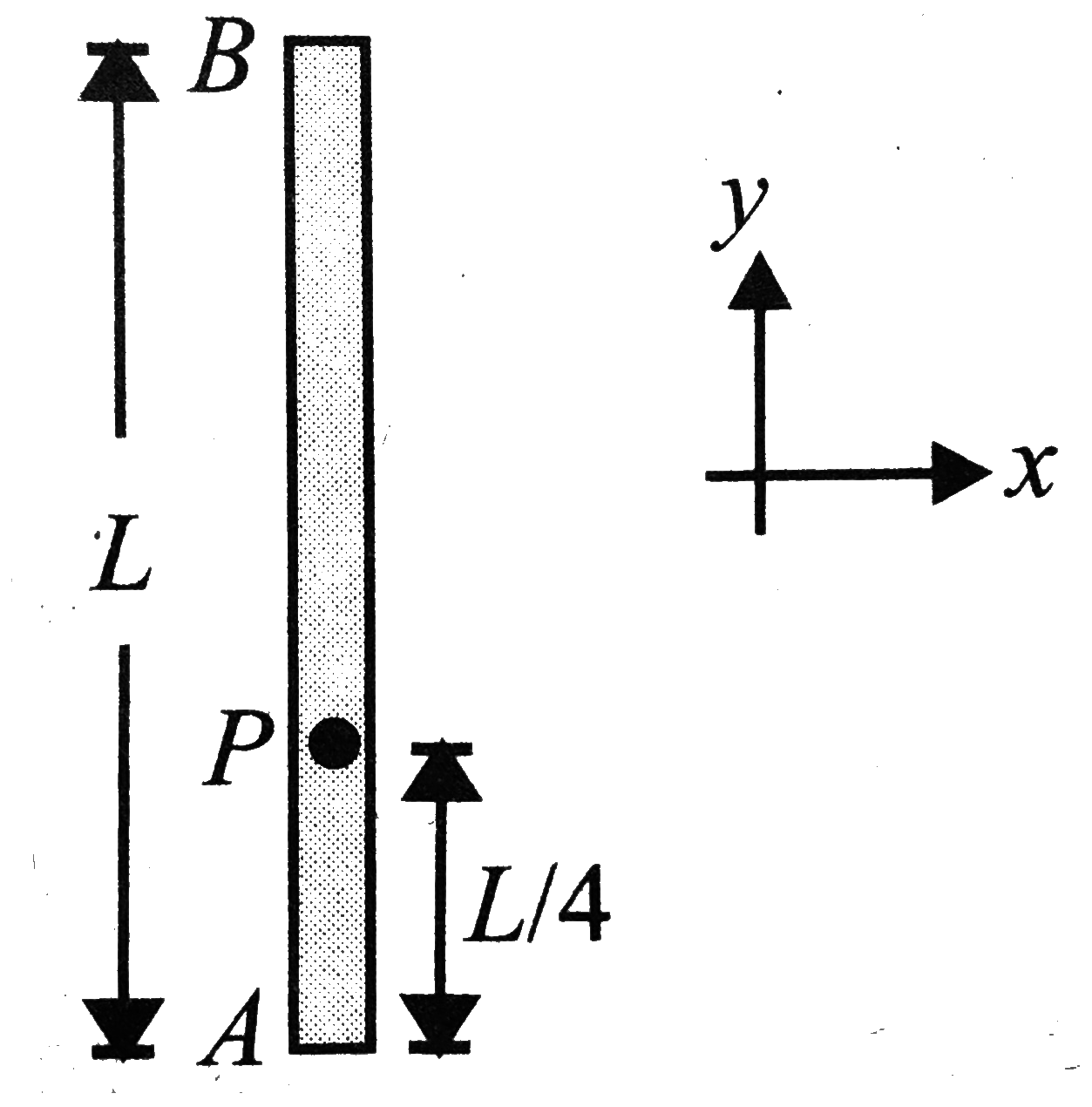
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......

Options

A. 1 . `w(d - x)/d` ,`wx/d`,
B. 2. `wd , wx/d`
C. 3. `wd, w(x-d)/d`
D. 4.`(xw/ d - x) , xw/d`

Answer

c

Explanation

To solve the problem, we need to determine the normal reactions at points A and B when a rod is supported by two parallel knife edges and is in equilibrium.

1. Identify Given Information:
- Weight of the rod, \( W \)
- Distance between the knife edges, \( d \)
- Distance from knife edge A to the center of mass of the rod, \( x \)
- Distance from knife edge B to the center of mass of the rod, \( d - x \)

2. Draw a Free Body Diagram:
- Represent the rod horizontally with knife edges A and B.
- Mark the normal reaction at A as \( N_1 \) and at B as \( N_2 \).
- The weight of the rod acts downwards at the center of mass.

3. Apply the Equilibrium Condition for Forces:
- Since the rod is in equilibrium, the sum of the vertical forces must be zero:
\( N_1 + N_2 = W \quad \text{(Equation 1)} \)

4. Apply the Equilibrium Condition for Moments:
- Taking moments about point A (the moment due to \( N_1 \) is zero as it acts at point A):
\( W \cdot x = N_2 \cdot d \)
- Rearranging gives:
\( N_2 = \frac{W \cdot x}{d} \quad \text{(Equation 2)} \)

5. Substitute \( N_2 \) into Equation 1:
- Substitute Equation 2 into Equation 1:
\( N_1 + \frac{W \cdot x}{d} = W \)
- Rearranging gives:
\( N_1 = W - \frac{W \cdot x}{d} \)
- Factor out \( W \):
\( N_1 = W \left(1 - \frac{x}{d}\right) = W \frac{d - x}{d} \quad \text{(Equation 3)} \)

6. Final Results:
- The normal reaction at A:
\( N_1 = W \frac{d - x}{d} \)
- The normal reaction at B:
\( N_2 = \frac{W \cdot x}{d} \)

Summary:
- The normal reaction on A is \( N_1 = W \frac{d - x}{d} \).
- The normal reaction on B is \( N_2 = \frac{W \cdot x}{d} \).