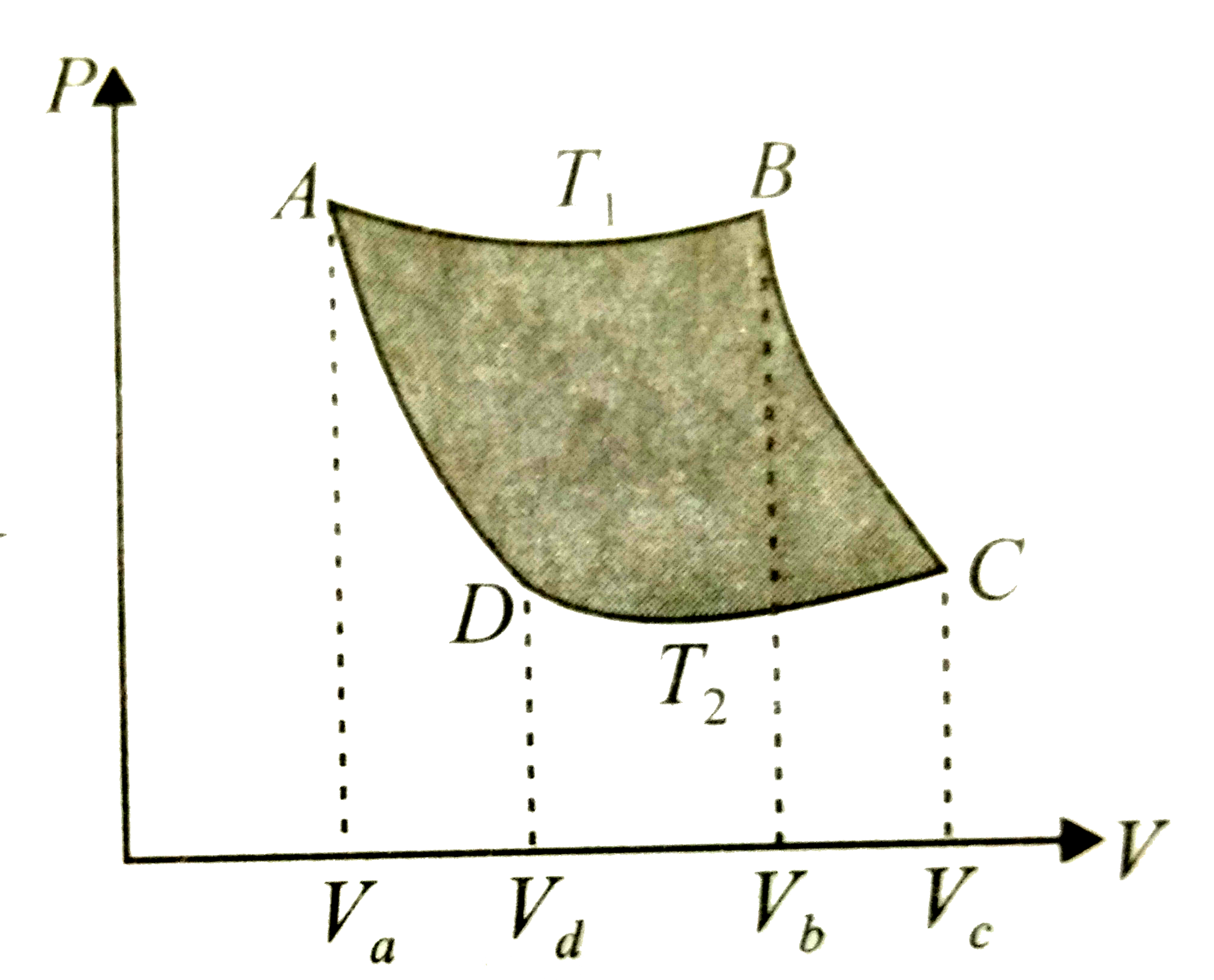
Two different adiabatic parts for the same gas intersect two isothermals at T1andT_2 as shown in P-V diagram . Then the ratio of VaVb will be
a. VcVd
b. VdVc
c. γVdVc
d. 1γVdVc
The correct Answer is:B
For adiabatic curve BC
T1Vγ−1b=T2Vγ−1C
Dividing (i) by (ii)
Vb(Va)γ−1=VC(Vd)γ−1⇒VaVb=VdVC
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
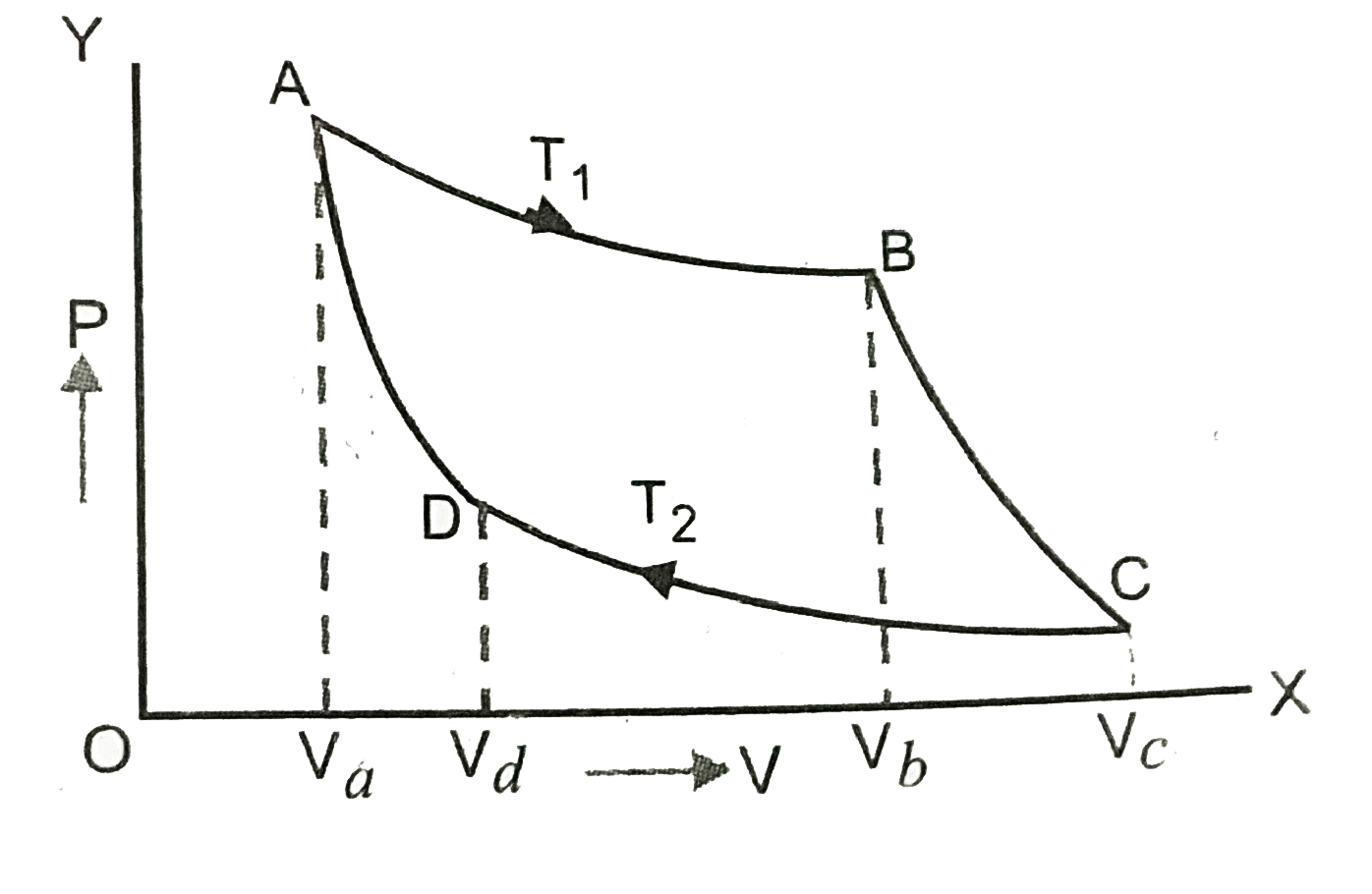
Two different adiabatic curves for the same gas intersect two isothermals at T1,andT2 as shown in P−V diagram, (figure). How does the ratio (Va/Vd) compare with the ratio (Vb/Vc) ?
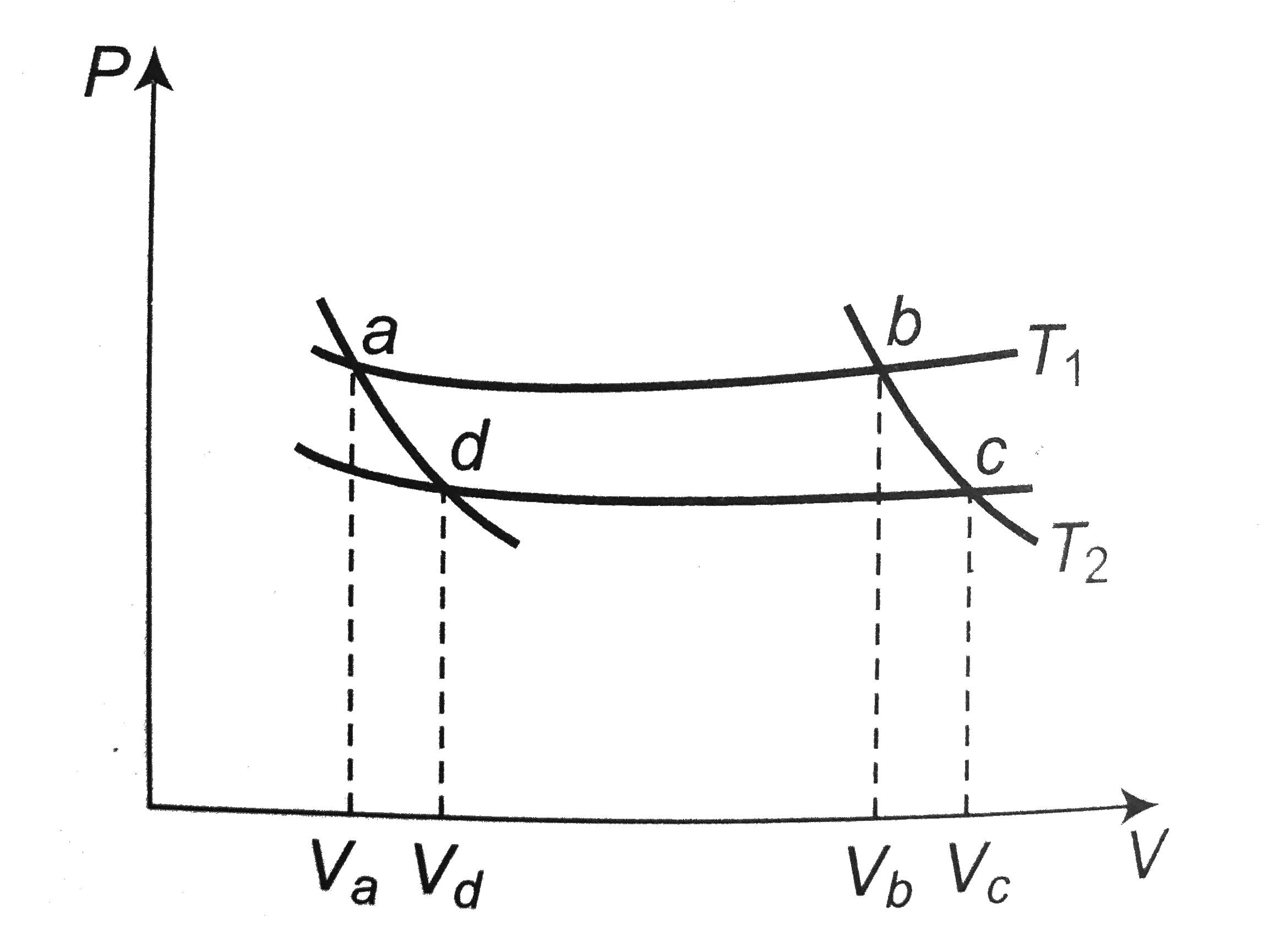
View SolutionIn the following P-V diagram two adiabatics cut two isothermals at temperature T1andT2 (fig). The value of VaVd will be
View Solution
Knowledge Check
1 mole of an ideal gas in a cylindrical container have the P-V diagram as shown in figure.If V2=4V1 then the ratio of temperatures T1T2 will be
 Aa. 12Bb.14Cc. 32Dd. 34
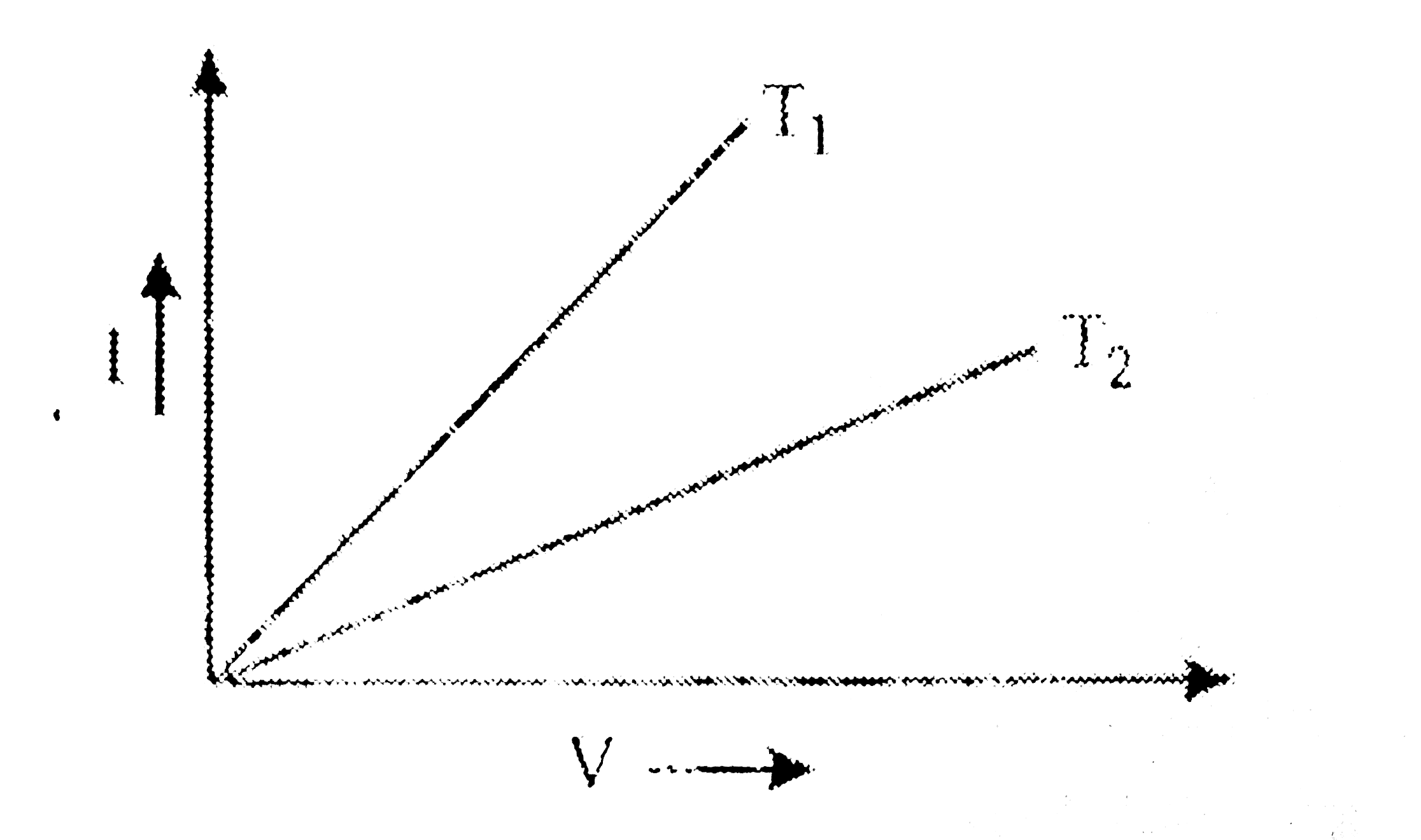
Aa. 12Bb.14Cc. 32Dd. 34The voltage V and current I v graphs for a conductor at two different temperatures T1andT2 are shown in the figure. The relation between T1andT2 is
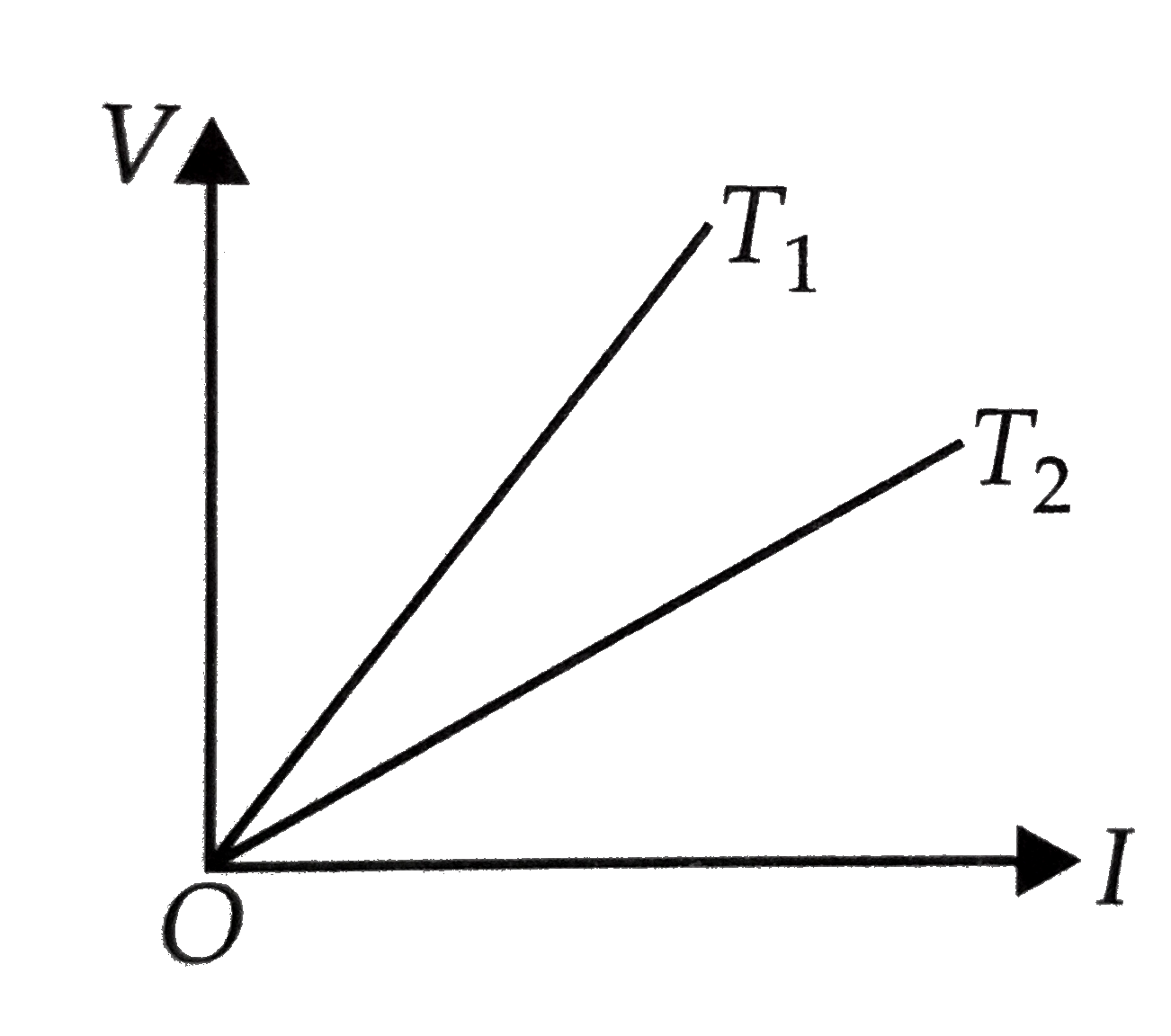 AT1>T2BT1<T2CT1=T2DT1=1T2
AT1>T2BT1<T2CT1=T2DT1=1T2
I-V graph for a metallie wire at two different tempearture, T1andT2 is as shown in the figure. Which of the two temperatures is lower and why ?
View SolutionAn ideal gas (1 mol ,monatomic) is in the initial state P (see diagram) on an isothermal curve A at a temperature T0 . It is brought under a constant volume (2V0) process to Q which lies on an adiabatic curve B intersecting the isothermal curve A at (P0,V0,T0) . The change in the internal energy of the gas (in terms of T0 ) during the process is (22/3=1.587)

View SolutionAn ideal gas (1 mol, monatomic) is in the intial state P (see Fig.) on an isothermal A at temperature T0. It is brought under a constant volume (2V0) process to Q which lies on an adiabatic B intersecting the isothermal A at (P0,V0,T0). The change in the internal energy of the gas during the process is (in terms of T0)(22/3=1.587)
View SolutionWrite down the relation for an adiabatic process in terms of (i) P and V (ii) T and V and (iii) P and T.
View SolutionA gas take part in two thermal processes in which it is heated from the same initial state to the same final temperature. The processes are shown on the P−V diagram by straight lines 1→3 and 1→2

View SolutionA gas take part in two thermal processes in which it is heated from the same initial state to the same final temperature. The processes are shown on the P−V diagram by straight lines 1→3 and 1→2

View Solution
