Write down the relation for an adiabatic process in terms of (i) P and V (ii) T and V and (iii) P and T.
To derive the relations for an adiabatic process in terms of pressure (P), volume (V), temperature (T), we can follow these steps:
Step 1: Relation between P and V
For an adiabatic process, the relation between pressure (P) and volume (V) is given by:
PVγ=constant
where γ (gamma) is the heat capacity ratio, defined as γ=CpCv.
Step 2: Relation between T and V
Using the ideal gas law, we know that:
PV=nRT
From this, we can express pressure (P) in terms of volume (V) and temperature (T):
P=nRTV
Substituting this expression for P into the adiabatic relation PVγ=constant:
(nRTV)Vγ=constant
This simplifies to:
nRTVγ−1=constant
Thus, we can express the relation between temperature (T) and volume (V) as:
TVγ−1=constant
Step 3: Relation between P and T
Again using the ideal gas law PV=nRT, we can express volume (V) in terms of P and T:
V=nRTP
Substituting this expression for V into the adiabatic relation PVγ=constant:
P(nRTP)γ=constant
This simplifies to:
P1−γ(nRT)γ=constant
Rearranging gives us the relation between pressure (P) and temperature (T):
P1−γTγ=constant
Summary of Relations
1. Relation between P and V:
PVγ=constant
2. Relation between T and V:
TVγ−1=constant
3. Relation between P and T:
P1−γTγ=constant
PVγ=constant
TVγ−1=constant
P1−γTγ=constant
Topper's Solved these Questions
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - VERY SHORT ANSWER QUESTIONS
17 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM FIRST LAW OF THERMODYNAMICS )
6 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - LONG ANSWER QUESTIONS
8 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
Similar Questions
Knowledge Check
The relation between internal energy U, pressure P and volume V of a gas in an adiabatic process is
U=a+bPV where a and b are constants. What is the effective value of adiabatic constant γ ?A1. abB2. b+1bC3. a+1aD4. ba
P-V plots for two gases during an adiabatic process are given in the figure:
Plot A and plot B should correspond to :
View SolutionShow that the slope of p−V diagram is greater for an adiabatic process as compared to an isothermal process.
View SolutionIf x is the amount of adsorbate and m is the amount of adsorbent, which of the following relation is related to adsorption process?
(a)xm = f(T) at constant p
(b) p = f(T) at constant (xm)
(c)xm=p×T
(d)xm = f(p) at constant T
View SolutionExamine the following plots and predict whether in (i) P1<P2andT1>T2 , in (ii) T1=T2<T3, in (iii) V1>V2,in(iv)P1>P2orP2>P1
_E01_267_Q01.png)
View SolutionAssertion: Isothermal and adiabatic, two processes are shown on p-V diagram. Process-1 is aidabatic and process-2 is isothermal.
Reason: At a given point, slope of adiabatic process =γ×slope of isothermal process.
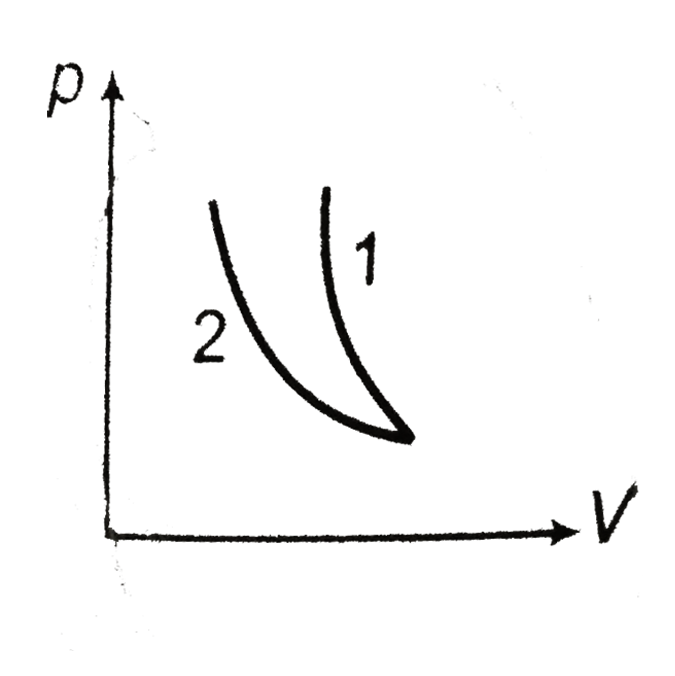
View SolutionAssertion: P v/s 1V graph is straight line for adiabatic process.
Reason: PV=constant for adiabatic process.
View SolutionDraw the P-T and V-T diagrams for an isobabaric process of expansion, corresponding to n moles of an ideal gas at pressure P0 from V0 to 2V0
View Solution
