Two points A and B located in diametrically opposite directions of a point charge of +2μC at distances 2.0 m and 1.0 m respectively from it. Determine the potential difference VA−VB
3×103V
6×104V
−9×103V
−3×103V
The correct Answer is:C
To determine the potential difference VA−VB between the points A and B located at distances of 2.0 m and 1.0 m respectively from a point charge of +2μC, we can follow these steps:
Step 1: Understand the formula for electric potential
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=kQr
where k is Coulomb's constant, approximately 8.99×109N m2/C2.
Step 2: Calculate the potential at point A
For point A, which is at a distance RA=2.0m:
VA=kQRA=(8.99×109)×(2×10−6)2
Calculating this:
VA=(8.99×109)×(2×10−6)2=(8.99×2)2×103=8.99×103V
Step 3: Calculate the potential at point B
For point B, which is at a distance RB=1.0m:
VB=kQRB=(8.99×109)×(2×10−6)1
Calculating this:
VB=(8.99×109)×(2×10−6)=17.98×103V
Step 4: Calculate the potential difference VA−VB
Now, we can find the potential difference:
VA−VB=8.99×103−17.98×103
Calculating this:
VA−VB=8.99×103−17.98×103=−8.99×103V
Final Result
Thus, the potential difference VA−VB is:
VA−VB=−8.99×103V
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=kQr
where k is Coulomb's constant, approximately 8.99×109N m2/C2.
For point A, which is at a distance RA=2.0m:
VA=kQRA=(8.99×109)×(2×10−6)2
Calculating this:
VA=(8.99×109)×(2×10−6)2=(8.99×2)2×103=8.99×103V
For point B, which is at a distance RB=1.0m:
VB=kQRB=(8.99×109)×(2×10−6)1
Calculating this:
VB=(8.99×109)×(2×10−6)=17.98×103V
Now, we can find the potential difference:
VA−VB=8.99×103−17.98×103
Calculating this:
VA−VB=8.99×103−17.98×103=−8.99×103V
Thus, the potential difference VA−VB is:
VA−VB=−8.99×103V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:HOTS
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXEMPLAR PROBLEMS
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTPS ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:MAGNETISM AND MATTER Exercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
Knowledge Check
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
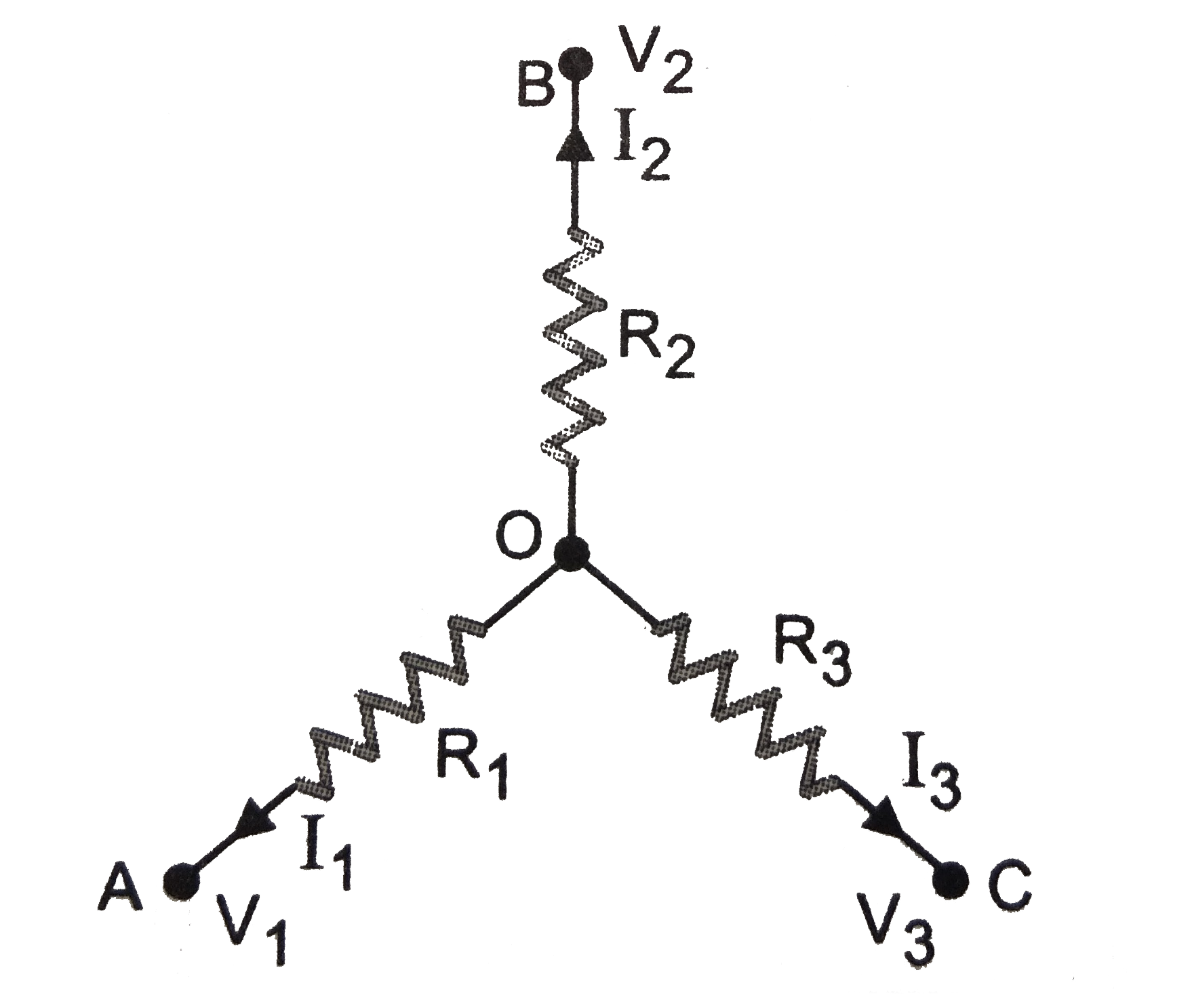 AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
AV1+V2+V3B[V1+V2+V3R1+R2+R3][1R1+R2+R3]−1CzeroD[V1+V2+V3R1+R2+R3](R1+R2+R3)
The work done in carrying a charge of 5μC form a point A to a point B in an electric field is 10mJ. The potential difference (VB−VA) is then
View SolutionPositive and negative charges of 1μC each are placed at two points as shown in the figure. Find the potential difference between A and B
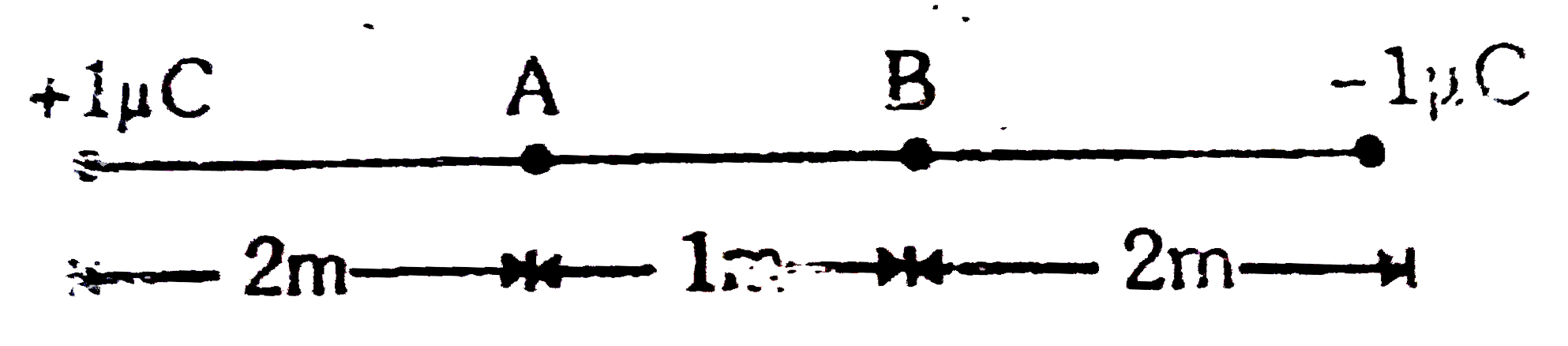
View SolutionIn the network shown in fig. , points A, B, and C are at potentials of 70 V, 0, and 10V, respectively.

View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
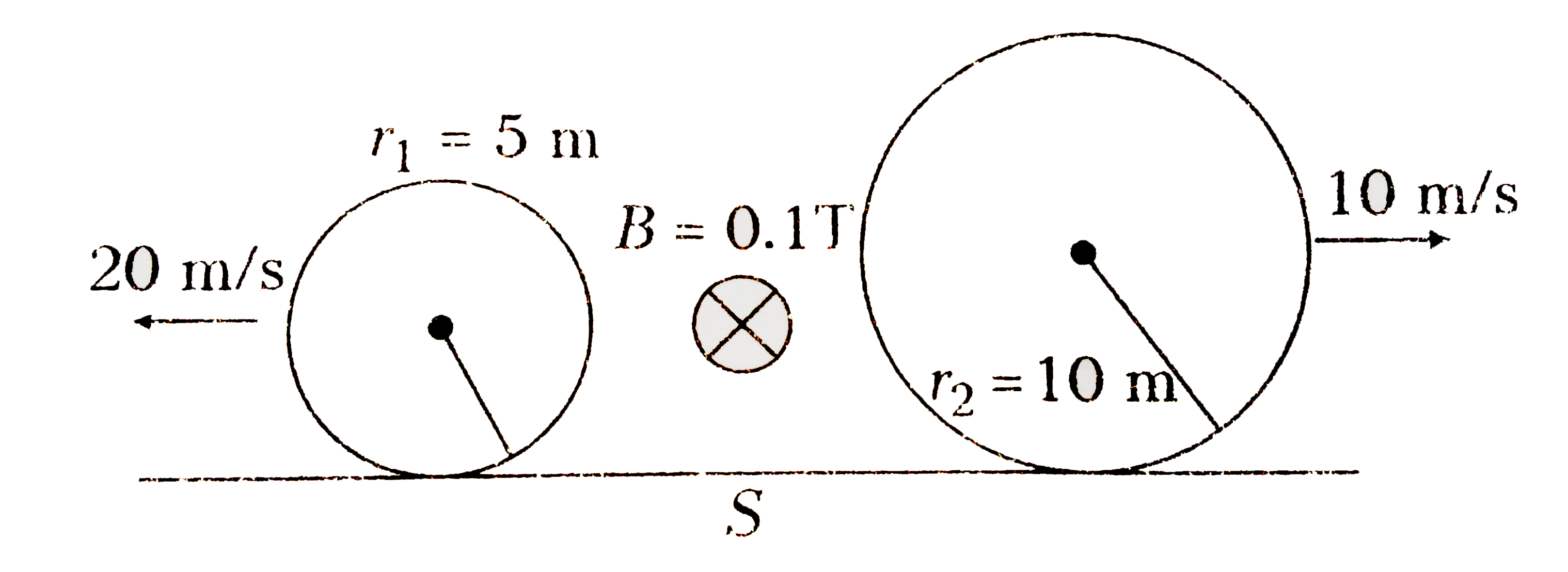
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
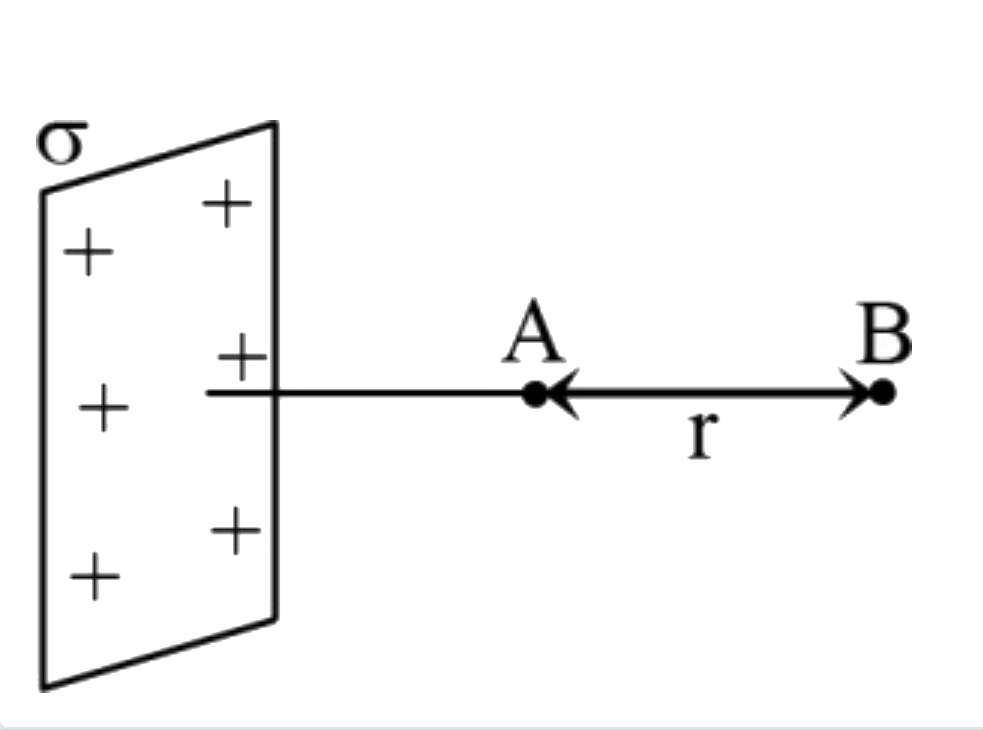
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).

View Solution
 .
.