Consider a uniform electric field in the ˆz direction. The potential is a constant.
for any x for a given z
for any y for a given z
on the x-y plane for a given z
All of these
The correct Answer is:D
To solve the problem regarding the uniform electric field in the ^z direction and the behavior of electric potential, we can follow these steps:
1. Understanding the Electric Field:
- We have a uniform electric field directed along the ^z axis. This means that the electric field →E can be expressed as:
→E=E^z
where E is a constant magnitude of the electric field.
2. Electric Potential and Electric Field Relationship:
- The relationship between electric potential V and electric field →E is given by:
→E=−∇V
This indicates that the electric field is the negative gradient of the electric potential. In simpler terms, the potential decreases in the direction of the electric field.
3. Potential Change in the z-direction:
- If we move in the direction of the electric field (which is along the ^z direction), the potential will change. Specifically, if we move a distance dz in the ^z direction, the change in potential dV can be expressed as:
dV=−Edz
This shows that the potential changes when we move in the ^z direction.
4. Potential Change in the x and y Directions:
- If we move in the x or y directions while keeping z constant, the potential does not change. This is because there is no displacement in the direction of the electric field. Therefore, for any movement in the xy plane (where z remains constant), the potential remains constant:
dV=0(for movement in the x or y direction)
5. Conclusion:
- Since the potential only changes when there is movement along the direction of the electric field (the ^z direction), and remains constant for movements in the x or y directions, we can conclude that the potential is constant for any motion that does not involve a change in the z coordinate.
Final Answer:
The potential is constant for any motion in the xy plane (i.e., when z is held constant).
- We have a uniform electric field directed along the ^z axis. This means that the electric field →E can be expressed as:
→E=E^z
where E is a constant magnitude of the electric field.
- The relationship between electric potential V and electric field →E is given by:
→E=−∇V
This indicates that the electric field is the negative gradient of the electric potential. In simpler terms, the potential decreases in the direction of the electric field.
- If we move in the direction of the electric field (which is along the ^z direction), the potential will change. Specifically, if we move a distance dz in the ^z direction, the change in potential dV can be expressed as:
dV=−Edz
This shows that the potential changes when we move in the ^z direction.
- If we move in the x or y directions while keeping z constant, the potential does not change. This is because there is no displacement in the direction of the electric field. Therefore, for any movement in the xy plane (where z remains constant), the potential remains constant:
dV=0(for movement in the x or y direction)
- Since the potential only changes when there is movement along the direction of the electric field (the ^z direction), and remains constant for movements in the x or y directions, we can conclude that the potential is constant for any motion that does not involve a change in the z coordinate.
The potential is constant for any motion in the xy plane (i.e., when z is held constant).
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A solid metal cube of edge length 2 cm is moving in a positive y-direction at a constant speed of 6 m/s. There is a uniform magnetic field of 0.1 T in the positive z-direction. The potential difference between the two faces of the cube perpendicular to the x-axis, is :
View SolutionA charged particle begins to move from the origin in a region which has a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. Its speed is v when it reaches the point (x, y, z). Then, v will depend
View Solution
Knowledge Check
Assertion : In a uniform electric field electrons move in the opposite direction of electric field.
Reason : This is because of the negative charge of an electron.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.Consider a uniform electric field E=3×103ˆiN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a 60∘ angle with the x-axis ?
A10NC−1m2B20NC−1m2C30NC−1m2D40NC−1m2
(A) : An electron moving with uniform velocity enters uniform magnetic field perpendicularly and then a uniform electric field in the same direction. Nature of paths followed by electron in both the fields will be same.
(R) : The force applied by magnetic and electric field on electron are in the same direction.
View Solution(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(b) Derive an expression for the electric potential at any point along the axial line of an electric dipole
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

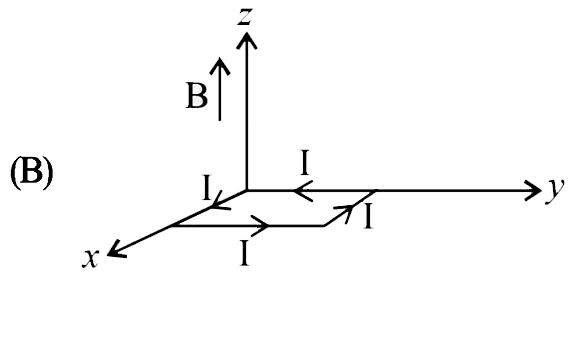

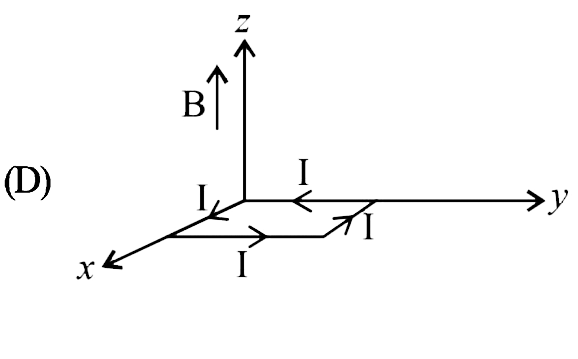
View SolutionAn electron traveling in a uniform electric field passes from a region of potential V1 to a region of higher potential V2. Then

View SolutionIn a uniform electric field if a charge is fired in a direction different from the line of electric field then the trajectory of the charge will be a
View SolutionConsider a uniform electric field E=3×103ˆiN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a 60∘ angle with the x-axis ?
View Solution
