A parallel plate condenser is charged by connected it to a battery. The battery is disconnected and a glass slab is introduced between the plates. Then
potential increases
electric intensity increases
energy decreases.
capacity decreases
The correct Answer is:B
To solve the problem step by step, we will analyze the situation of a parallel plate capacitor being charged, disconnected from a battery, and then having a glass slab introduced between the plates.
Step 1: Understand the Initial Condition
Initially, the parallel plate capacitor is connected to a battery. When connected, it charges up to a certain voltage V and stores a charge Q. The capacitance C of the capacitor is given by the formula:
C=Aϵ0D
where:
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- D is the separation between the plates.
Hint: Remember that capacitance depends on the physical characteristics of the capacitor and the medium between the plates.
Step 2: Disconnect the Battery
Once the capacitor is fully charged, the battery is disconnected. This means that the charge Q on the capacitor remains constant because it is now an isolated system.
Hint: The charge remains constant when the capacitor is isolated from any external circuit.
Step 3: Introduce the Glass Slab
When a glass slab is introduced between the plates, the capacitance of the capacitor changes. The new capacitance C′ with the glass slab is given by:
C′=k⋅C=kAϵ0D
where k is the dielectric constant of the glass, which is greater than 1.
Hint: The introduction of a dielectric increases the capacitance of the capacitor.
Step 4: Analyze the Effect on Voltage
Since the charge Q remains constant and the capacitance has increased, we can use the relationship between charge, capacitance, and voltage:
V=QC
With the new capacitance C′:
V′=QC′
Since C′>C, it follows that V′<V. Therefore, the voltage across the capacitor decreases.
Hint: An increase in capacitance with constant charge results in a decrease in voltage.
Step 5: Analyze the Electric Field
The electric field E between the plates is given by:
E=VD
Since the voltage V′ decreases and the distance D remains constant, the electric field E′ will also decrease:
E′=V′D
Hint: A decrease in voltage while keeping the distance constant leads to a decrease in electric field strength.
Step 6: Analyze the Energy Stored
The energy U stored in the capacitor can be expressed as:
U=12CV2
With the new capacitance and voltage, the energy becomes:
U′=12C′V′2
Since C′>C and V′<V, we can conclude that the energy stored in the capacitor decreases.
Hint: Energy stored in a capacitor is related to both capacitance and voltage; changes in either can affect the total energy.
Conclusion
- The capacitance increases when the glass slab is introduced.
- The voltage across the capacitor decreases.
- The electric field strength decreases.
- The energy stored in the capacitor decreases.
Summary of Options
1. The capacitance does not decrease; it increases.
2. The electric field decreases.
3. The energy stored decreases.
Thus, the correct conclusion is that the energy stored in the capacitor decreases.
Initially, the parallel plate capacitor is connected to a battery. When connected, it charges up to a certain voltage V and stores a charge Q. The capacitance C of the capacitor is given by the formula:
C=Aϵ0D
where:
- A is the area of the plates,
- ϵ0 is the permittivity of free space,
- D is the separation between the plates.
Once the capacitor is fully charged, the battery is disconnected. This means that the charge Q on the capacitor remains constant because it is now an isolated system.
When a glass slab is introduced between the plates, the capacitance of the capacitor changes. The new capacitance C′ with the glass slab is given by:
C′=k⋅C=kAϵ0D
where k is the dielectric constant of the glass, which is greater than 1.
Since the charge Q remains constant and the capacitance has increased, we can use the relationship between charge, capacitance, and voltage:
V=QC
With the new capacitance C′:
V′=QC′
Since C′>C, it follows that V′<V. Therefore, the voltage across the capacitor decreases.
The electric field E between the plates is given by:
E=VD
Since the voltage V′ decreases and the distance D remains constant, the electric field E′ will also decrease:
E′=V′D
The energy U stored in the capacitor can be expressed as:
U=12CV2
With the new capacitance and voltage, the energy becomes:
U′=12C′V′2
Since C′>C and V′<V, we can conclude that the energy stored in the capacitor decreases.
- The capacitance increases when the glass slab is introduced.
- The voltage across the capacitor decreases.
- The electric field strength decreases.
- The energy stored in the capacitor decreases.
1. The capacitance does not decrease; it increases.
2. The electric field decreases.
3. The energy stored decreases.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionA parallel plate capacitor is charged by a battery, which is then disconnected. A dielectric slab is now introduced between the two plates to occupy the space completely. State the effect on the following:
(i) the capacitance of the capacitor.
(ii) potential difference between the plates.
(iii) the energy stored in the capacitor.
View SolutionA parallel plate capacitor is charged by a battery. After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates. How will (i) the capacitance of the capacitor, (ii) potential difference between the plates and (iii) the energy stored in the capacitor be affected ?
Justify your answer in each case.
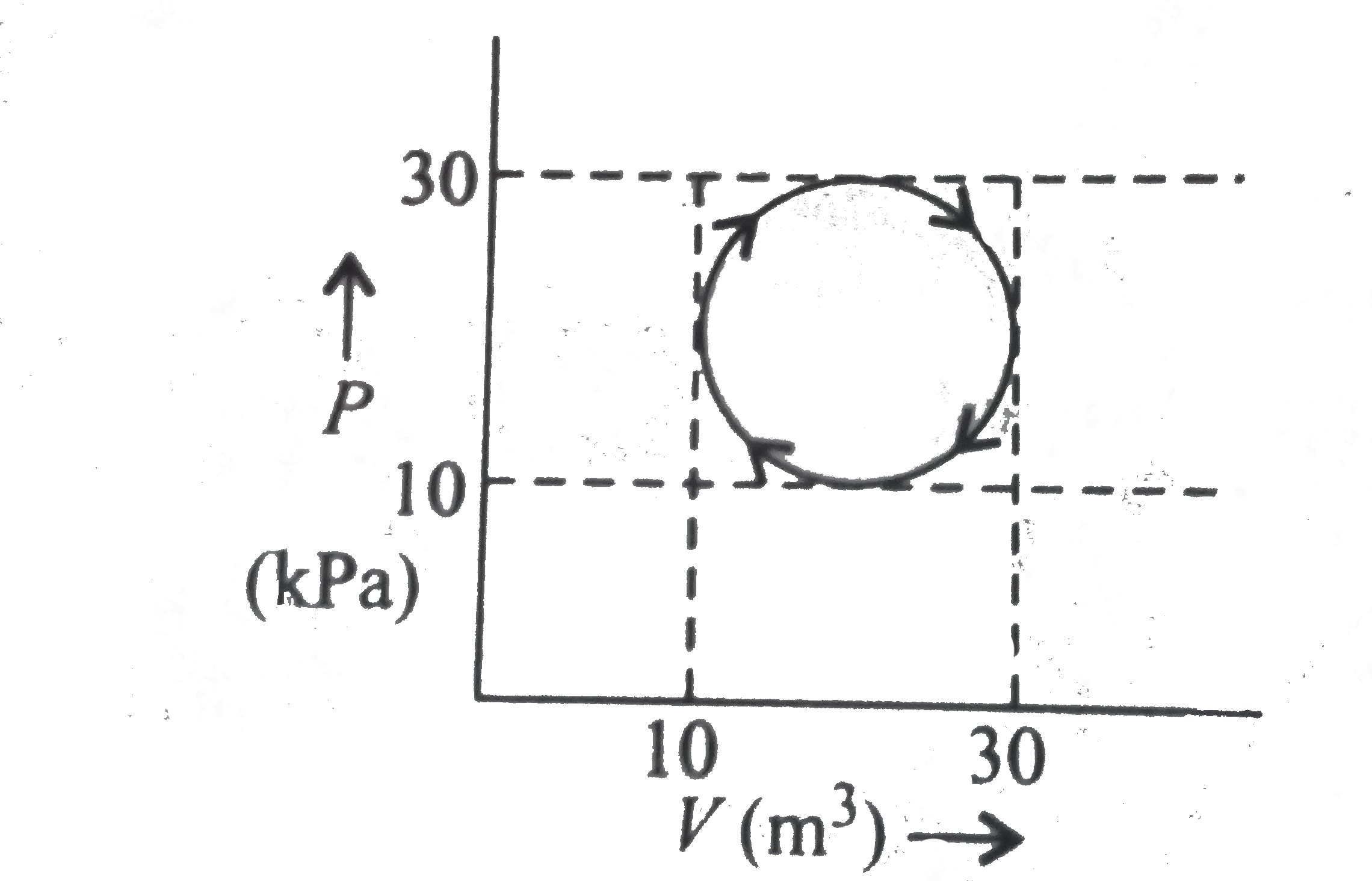
View SolutionWhich one is not correct for a cyclic process as shown in the figure ?
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionA parallel plate air capacitor is connected to a battery. After charging fully, the battery is disconnected and the plates are pulled apart to increase their separation. Which of the following statements is correct ?
View SolutionA parallel plate capacitor is connected to a battery. The plates are pulled apart with uniform speed. If x is the separation between the plates, then the rate of change of electrostatic energy of the capacitor is proportional to
View SolutionA parallel plate capacitor is charged and then the battery is disconnected. When the plates of the capacitor are brought closer, then
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
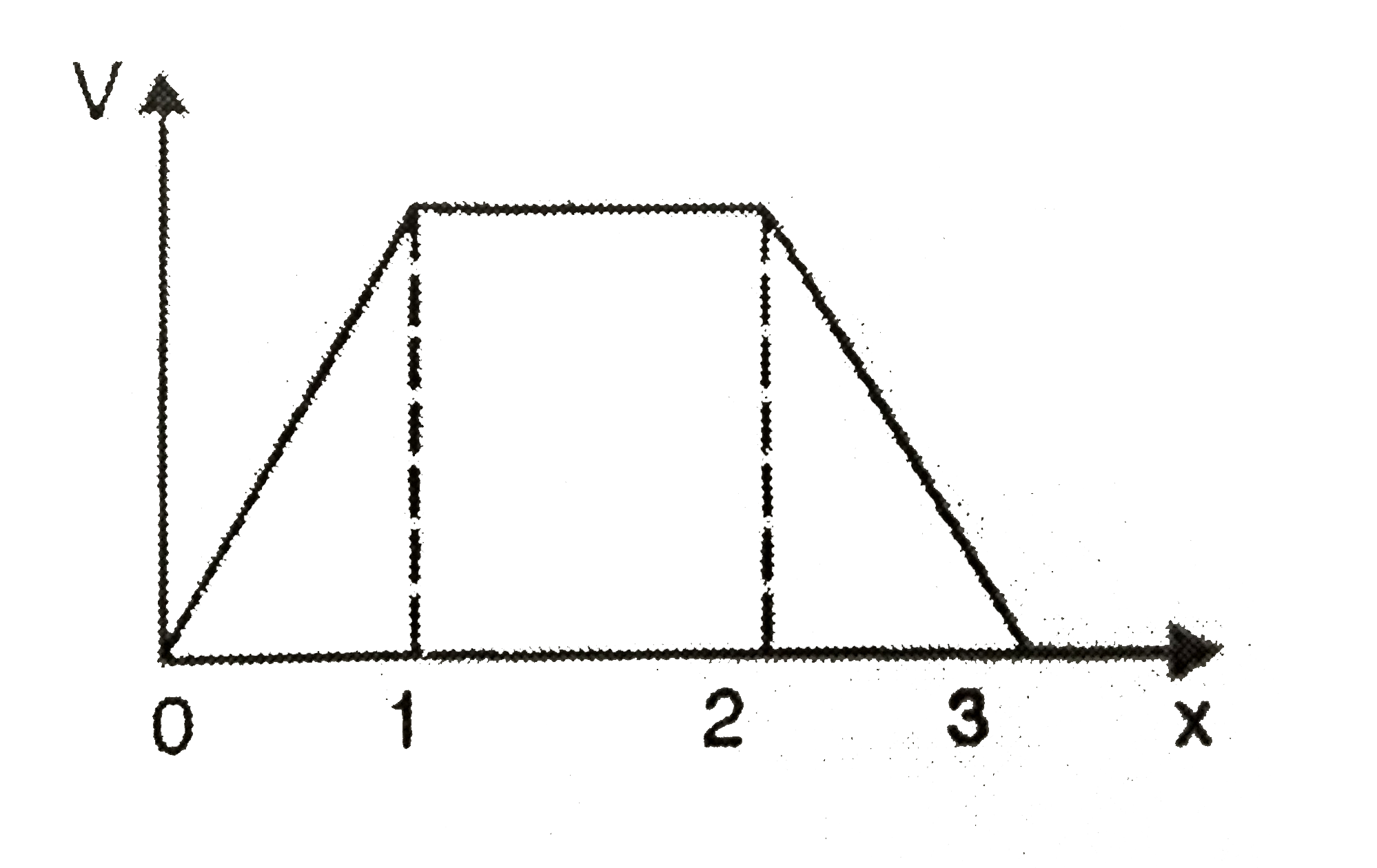
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
View Solution
