A current of 10 ampere is flowing in a wire of length 1.5m. A force of 15N acts on it when it is placed in a uniform magnetic field of 2 tesla. The angle between the magnetic field and the direction of the current is
30∘
45∘
60∘
90∘
The correct Answer is:A
To solve the problem, we need to find the angle θ between the magnetic field and the direction of the current using the formula for the force acting on a current-carrying conductor in a magnetic field.
1. Identify the Given Values:
- Current, I=10A
- Length of the wire, L=1.5m
- Magnetic field strength, B=2T
- Force acting on the wire, F=15N
2. Use the Formula for Magnetic Force:
The magnetic force F on a current-carrying wire is given by the formula:
F=BILsinθ
where:
- F is the force,
- B is the magnetic field strength,
- I is the current,
- L is the length of the wire,
- θ is the angle between the magnetic field and the current.
3. Rearrange the Formula to Solve for sinθ:
We can rearrange the formula to isolate sinθ:
sinθ=FBIL
4. Substitute the Known Values:
Now, substitute the values into the equation:
sinθ=15N(2T)(10A)(1.5m)
5. Calculate the Denominator:
Calculate the product in the denominator:
BIL=2×10×1.5=30T.A.m
6. Calculate sinθ:
Now substitute this back into the equation:
sinθ=1530=12
7. Determine θ:
To find θ, we take the inverse sine:
θ=sin−1(12)
From trigonometric values, we know:
θ=30∘
Final Answer:
The angle θ between the magnetic field and the direction of the current is 30∘.
---
- Current, I=10A
- Length of the wire, L=1.5m
- Magnetic field strength, B=2T
- Force acting on the wire, F=15N
The magnetic force F on a current-carrying wire is given by the formula:
F=BILsinθ
where:
- F is the force,
- B is the magnetic field strength,
- I is the current,
- L is the length of the wire,
- θ is the angle between the magnetic field and the current.
We can rearrange the formula to isolate sinθ:
sinθ=FBIL
Now, substitute the values into the equation:
sinθ=15N(2T)(10A)(1.5m)
Calculate the product in the denominator:
BIL=2×10×1.5=30T.A.m
Now substitute this back into the equation:
sinθ=1530=12
To find θ, we take the inverse sine:
θ=sin−1(12)
From trigonometric values, we know:
θ=30∘
The angle θ between the magnetic field and the direction of the current is 30∘.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
The force exerted on a current-carrying wire placed in magnetic field is zero when the angle between the wire and the direction of magnetic field is :
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
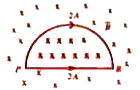 View Solution
View SolutionThe magnetic field at the origin due to the current flowing in the wire is
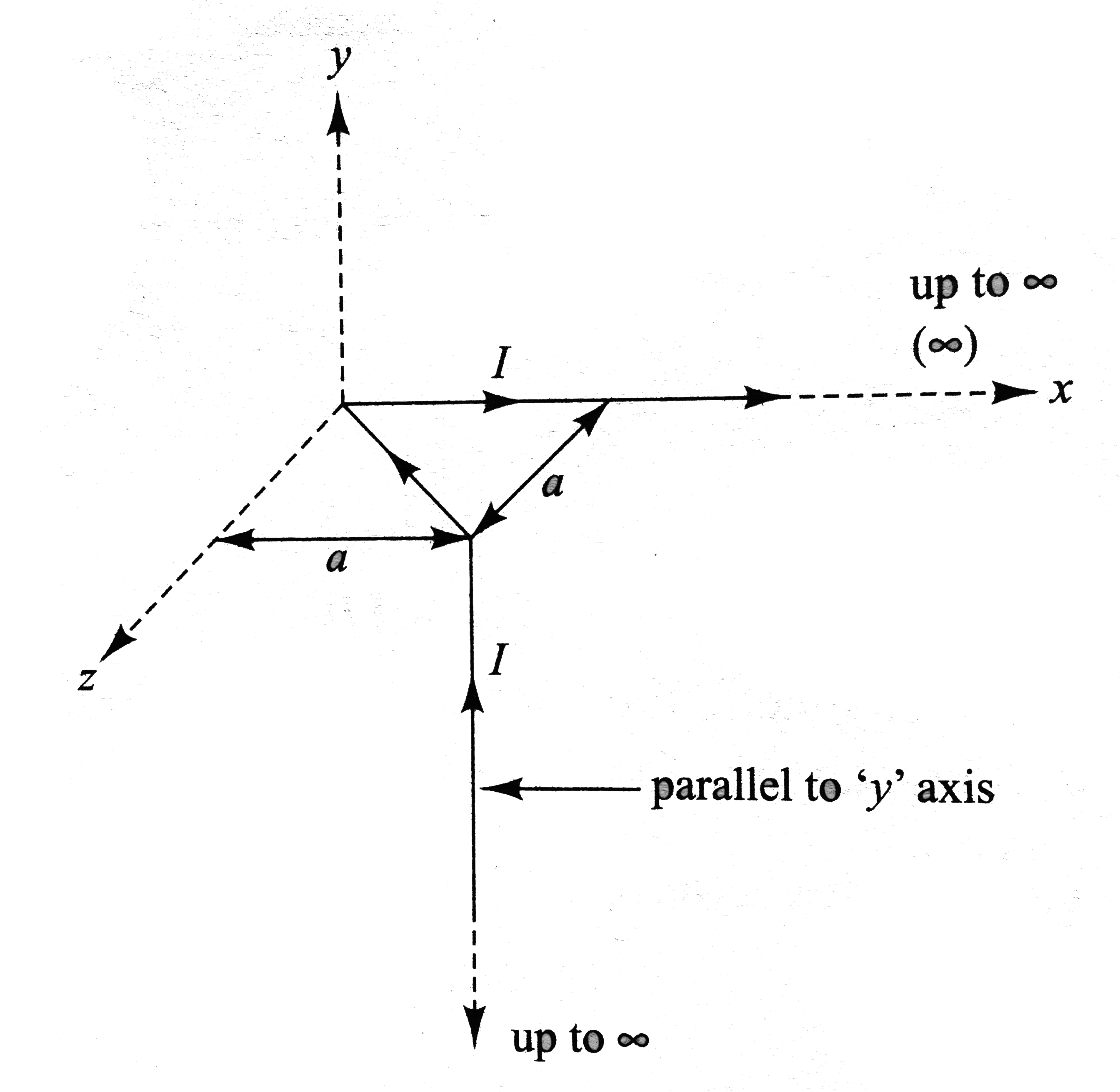 View Solution
View SolutionThe magnetic field at the origin due to the current flowing in the wire is
 View Solution
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionIf a wire of length l meter placed in uniform magnetic field 1.5 Tesla at angle 30∘ with magnetic field. The current in a wire 10 amp. Then force on a wire will be
View Solution

