Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?

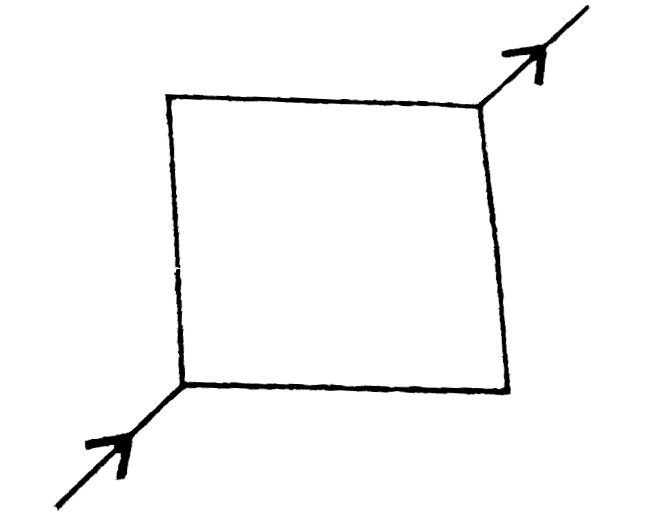


The correct Answer is:C
To determine in which case the magnetic field at the center of a uniform square frame is not zero, we will analyze each option using the right-hand thumb rule. This rule helps us find the direction of the magnetic field produced by a current-carrying conductor.
1. Understanding the Right-Hand Thumb Rule:
- The right-hand thumb rule states that if you point your thumb in the direction of the current, the curl of your fingers will indicate the direction of the magnetic field lines around the conductor.
2. Analyzing Each Option:
- We will consider the current direction in each section of the square frame and determine the resultant magnetic field at the center.
3. Option 1:
- In this option, the current enters one junction and exits another.
- For the sections:
- Section 1: Current flowing inwards (magnetic field directed into the center).
- Section 3: Current flowing outwards (magnetic field directed out of the center).
- The magnetic fields from sections 1 and 3 cancel each other out, resulting in zero net magnetic field.
- Sections 2 and 4: Both have outward magnetic fields, which add up.
- Therefore, the net magnetic field at the center is non-zero.
4. Option 2:
- Similar to option 1, the current flows in such a way that:
- Sections 1 and 3: Cancel each other out.
- Sections 2 and 4: Both have outward magnetic fields, which add up.
- Thus, the net magnetic field at the center is also non-zero.
5. Option 3:
- Current flows in a manner where:
- Sections 1 and 3: Magnetic fields cancel each other out.
- Sections 2 and 4: Magnetic fields also cancel each other out.
- Therefore, the net magnetic field at the center is zero.
6. Option 4:
- The current flows in such a way that:
- Sections 1 and 3: Magnetic fields cancel each other out.
- Sections 2 and 4: Magnetic fields also cancel each other out.
- Thus, the net magnetic field at the center is zero.
Conclusion:
The magnetic field at the center of the frame is not zero in Option 1 and Option 2.
- The right-hand thumb rule states that if you point your thumb in the direction of the current, the curl of your fingers will indicate the direction of the magnetic field lines around the conductor.
- We will consider the current direction in each section of the square frame and determine the resultant magnetic field at the center.
- In this option, the current enters one junction and exits another.
- For the sections:
- Section 1: Current flowing inwards (magnetic field directed into the center).
- Section 3: Current flowing outwards (magnetic field directed out of the center).
- The magnetic fields from sections 1 and 3 cancel each other out, resulting in zero net magnetic field.
- Sections 2 and 4: Both have outward magnetic fields, which add up.
- Therefore, the net magnetic field at the center is non-zero.
- Similar to option 1, the current flows in such a way that:
- Sections 1 and 3: Cancel each other out.
- Sections 2 and 4: Both have outward magnetic fields, which add up.
- Thus, the net magnetic field at the center is also non-zero.
- Current flows in a manner where:
- Sections 1 and 3: Magnetic fields cancel each other out.
- Sections 2 and 4: Magnetic fields also cancel each other out.
- Therefore, the net magnetic field at the center is zero.
- The current flows in such a way that:
- Sections 1 and 3: Magnetic fields cancel each other out.
- Sections 2 and 4: Magnetic fields also cancel each other out.
- Thus, the net magnetic field at the center is zero.
The magnetic field at the center of the frame is not zero in Option 1 and Option 2.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
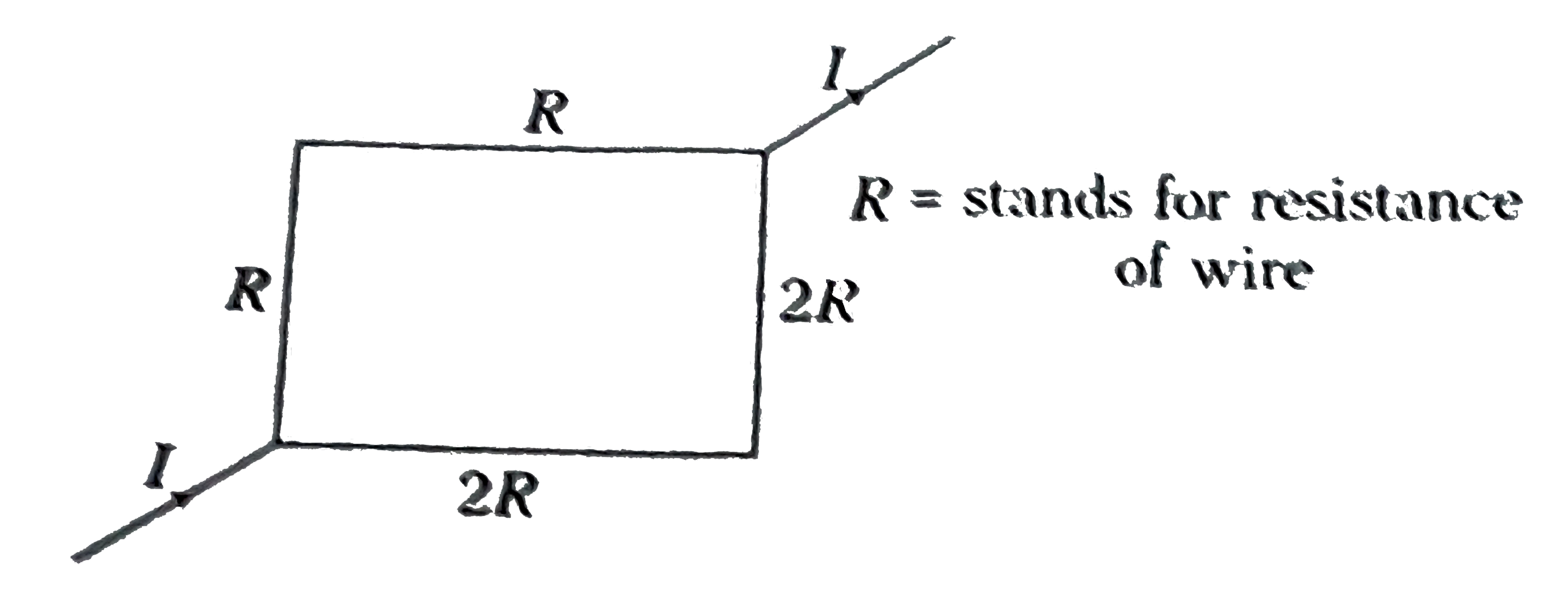
The magnetic field at the centre of square of side a is
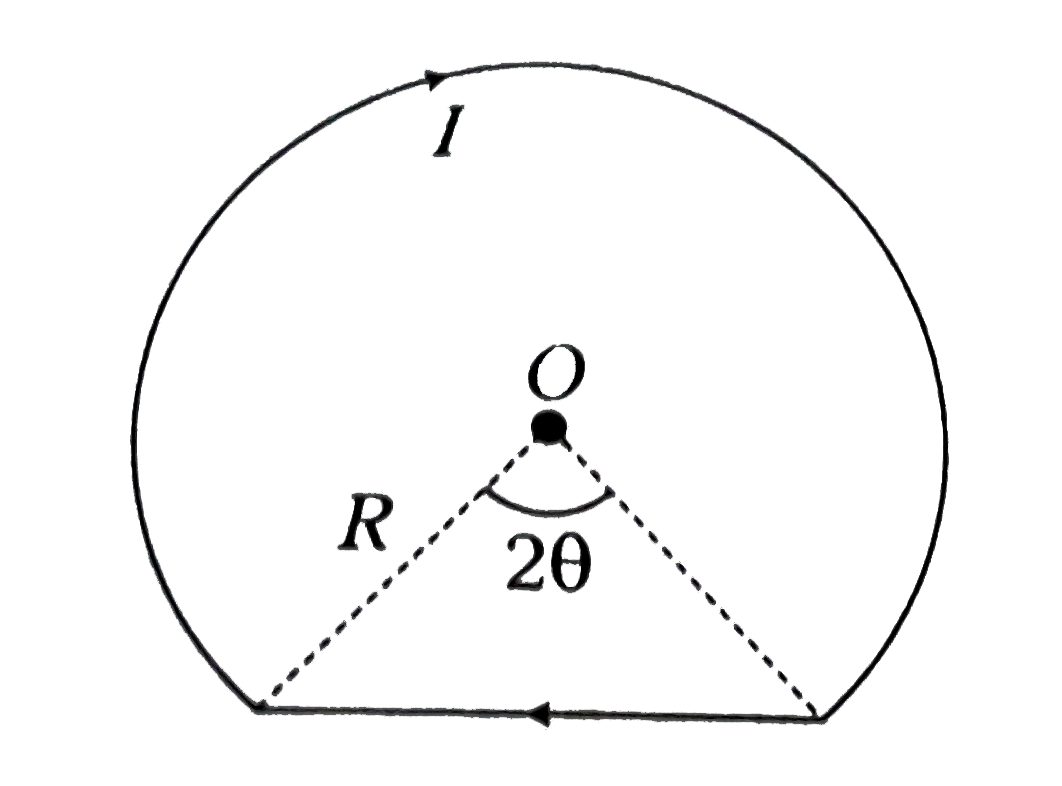
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
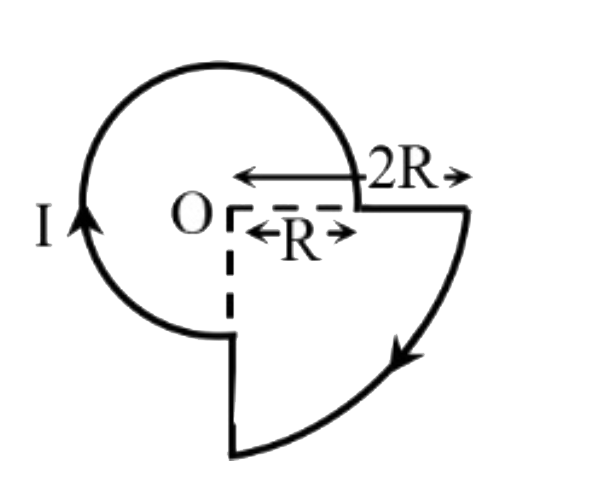
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,

View SolutionIf current through a circular coil flows in clockwise direction, then the direction of magnetic field at the centre of the circular coil is………………to the plane of the coil, directed……………. .
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionFour very long wires are arranged as shown in the figure, so that their cross - section forms a square, with connections at the ends so that current I flow through all four wires. Length of each side of the formed such square is b. The magnetic field at the central point P (centre of the square) is
View Solution
