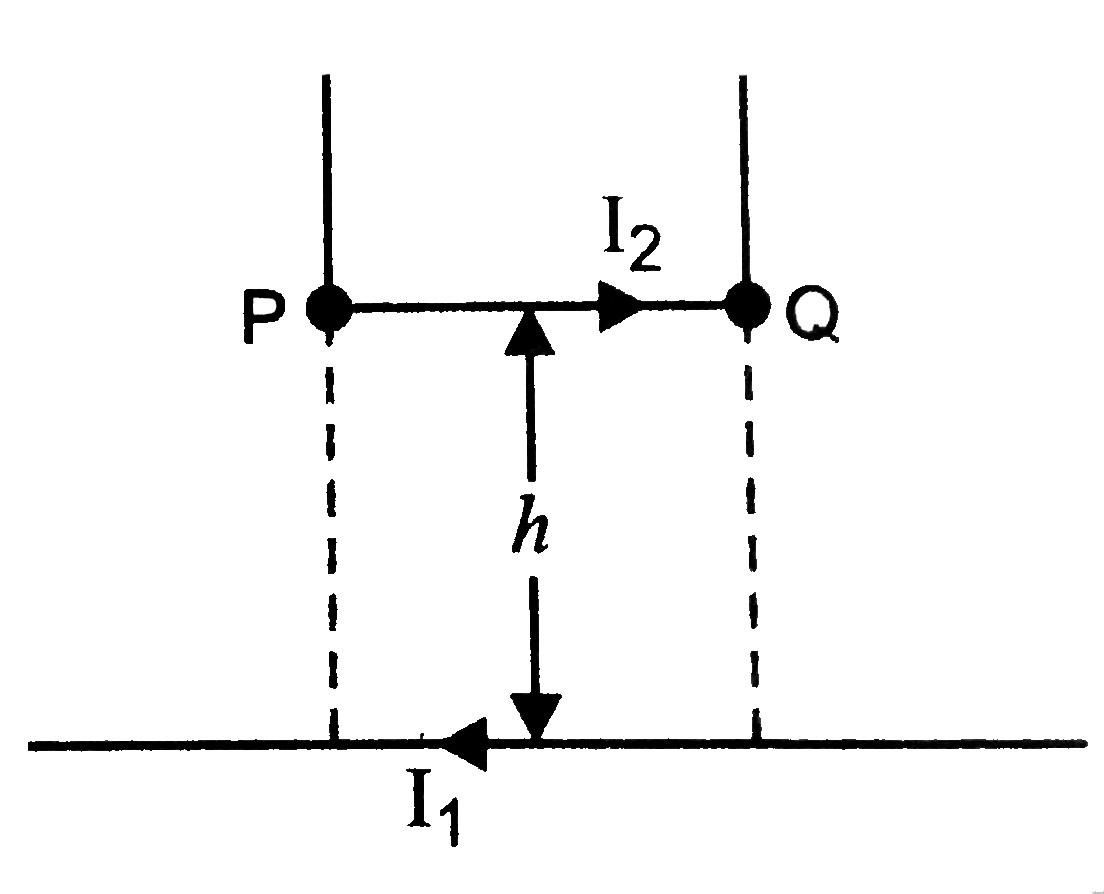
A long straight wire carrying current of 30 A rests on a table. Another wire AB of length 1 m, mass 3 g carries the same current but in the opposite direction, the wire AB is free to slide up and down. The height upto which AB will rise is
0.6 cm
0.7 cm
0.4 cm
0.5 cm
The correct Answer is:A
To solve the problem of how high the wire AB will rise, we will follow these steps:
Step 1: Understand the Forces Acting on Wire AB
The wire AB is subjected to two main forces:
1. The gravitational force acting downward, which is given by Fg=mg.
2. The magnetic force acting upward due to the interaction with the long straight wire PQ, which is given by the formula for the magnetic force between two parallel currents.
Step 2: Calculate the Gravitational Force
Given:
- Mass of wire AB, m=3g=3×10−3kg
- Acceleration due to gravity, g=9.8m/s2
The gravitational force Fg can be calculated as:
Fg=mg=(3×10−3kg)(9.8m/s2)=2.94×10−2N
Step 3: Calculate the Magnetic Force
The magnetic force Fm between two parallel wires carrying current can be calculated using the formula:
Fm=μ0I1I2L2πh
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I1=I2=30A (currents in both wires)
- L=1m (length of wire AB)
- h is the height we want to find.
Step 4: Set the Forces Equal in Equilibrium
At equilibrium, the magnetic force equals the gravitational force:
Fm=Fg
Substituting the expressions for the forces:
μ0I1I2L2πh=mg
Step 5: Rearranging to Solve for Height h
Rearranging the equation to solve for h:
h=μ0I1I2L2πmg
Step 6: Substitute the Known Values
Substituting the known values into the equation:
h=(4π×10−7T m/A)(30A)(30A)(1m)2π(3×10−3kg)(9.8m/s2)
Step 7: Simplify the Equation
h=(4×10−7)(30)(30)2(3×10−3)(9.8)
Calculating the numerator:
4×30×30=3600×10−7
Calculating the denominator:
2×3×10−3×9.8=58.8×10−3
Thus:
h=3600×10−758.8×10−3=360058.8×10−4≈61.22×10−4m=0.6122cm
Final Result
The height up to which wire AB will rise is approximately:
h≈0.6122cm≈0.6cm
The wire AB is subjected to two main forces:
1. The gravitational force acting downward, which is given by Fg=mg.
2. The magnetic force acting upward due to the interaction with the long straight wire PQ, which is given by the formula for the magnetic force between two parallel currents.
Given:
- Mass of wire AB, m=3g=3×10−3kg
- Acceleration due to gravity, g=9.8m/s2
Fg=mg=(3×10−3kg)(9.8m/s2)=2.94×10−2N
The magnetic force Fm between two parallel wires carrying current can be calculated using the formula:
Fm=μ0I1I2L2πh
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I1=I2=30A (currents in both wires)
- L=1m (length of wire AB)
- h is the height we want to find.
At equilibrium, the magnetic force equals the gravitational force:
Fm=Fg
Substituting the expressions for the forces:
μ0I1I2L2πh=mg
Rearranging the equation to solve for h:
h=μ0I1I2L2πmg
Substituting the known values into the equation:
h=(4π×10−7T m/A)(30A)(30A)(1m)2π(3×10−3kg)(9.8m/s2)
h=(4×10−7)(30)(30)2(3×10−3)(9.8)
Calculating the numerator:
4×30×30=3600×10−7
Calculating the denominator:
2×3×10−3×9.8=58.8×10−3
Thus:
h=3600×10−758.8×10−3=360058.8×10−4≈61.22×10−4m=0.6122cm
The height up to which wire AB will rise is approximately:
h≈0.6122cm≈0.6cm
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A long straight wire carrying current of 25A rests on a table as shown in figure. Another wire PQ of length 1m, mass 2⋅5g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?
View SolutionA straight wire of diametre 0.5 mm carrying a current of 1 A is replaced by another wire of 1mm diametre carrying same current. The strenth of magnetic field far away is
View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
A long straight wire carries a current of 35A. What is the magnitude of the field →B at a point 20cm from the wire?
View SolutionA long straight wire is carrying a current of 25 A. A squre loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is

View SolutionA long, straight wire carries a current. Is Ampere's law
valid for a loop that does not enclose the wire, or that
encloses the wire but is not circular?
View SolutionA thin circular wire carrying a current I has a magnetic moment M. The shape of the wire is changed to a square and it carries the same current. It will have a magnetic moment
View SolutionA straight wilre of diameter 0.5mm carrying a current 2A is replaced by another wire of diameter 1mm carrying the same current. The strength of magnetic field at a distance 2m away from the centre is
View SolutionInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point P is
 .
.
View SolutionAn infinitely long straight wire is carrying a current I1. Adjacent to it there is another equilateral triangular wire having current I2. Choose the wrong options
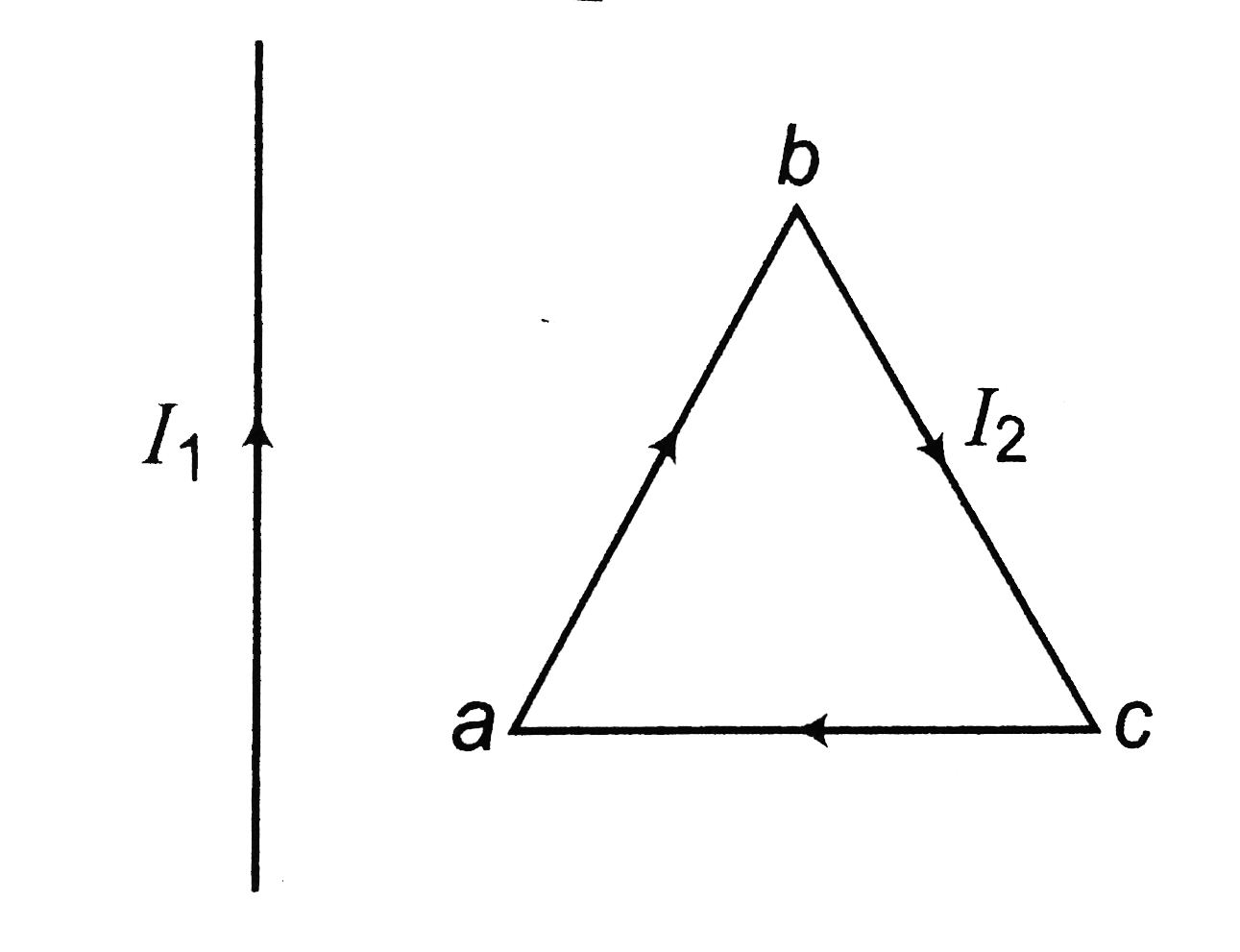
View Solution
