A square of side x m lies in the x-y plane in a region, when the magntic field is given by →B=B0(3ˆi+4ˆj+5ˆk) T, where B0 is constant. The magnitude of flux passing through the square is
5B0x2Wb
3B0x3Wb
2B0x2Wb
B0x2Wb
The correct Answer is:A
Here, →A=x2ˆkm2and→B=B0(3ˆi+4ˆj+5ˆk)T
AS ϕ=→B.→A=B0(3ˆi+4ˆj+5ˆk).x2ˆk
∴ϕ=5B0x2Wb
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS3videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON15videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason15videos
ELECTROMAGNETIC WAVES
Similar Questions
A square of side L meters lies in the x-y plane in a region, where the magnetic field is given by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by =B0(2ˆi+3ˆj+4ˆk)T,, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is give by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
View SolutionA square of side 'a' is lying in xy plane such that two of its sides are lying on the axis. If an electric field →E=E0xˆk is applied on the square. The flux passing through the square is :
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionA rectangular wire loop with length a and width b lies in the xy - plane as shown. Within the loop, there is a time dependent magnetic field given by →B=c[(xcosωt)ˆi+(ysinωt)ˆk]. Here, c and ω are constants. The magnitude of emf induced in the loop as a function of time is
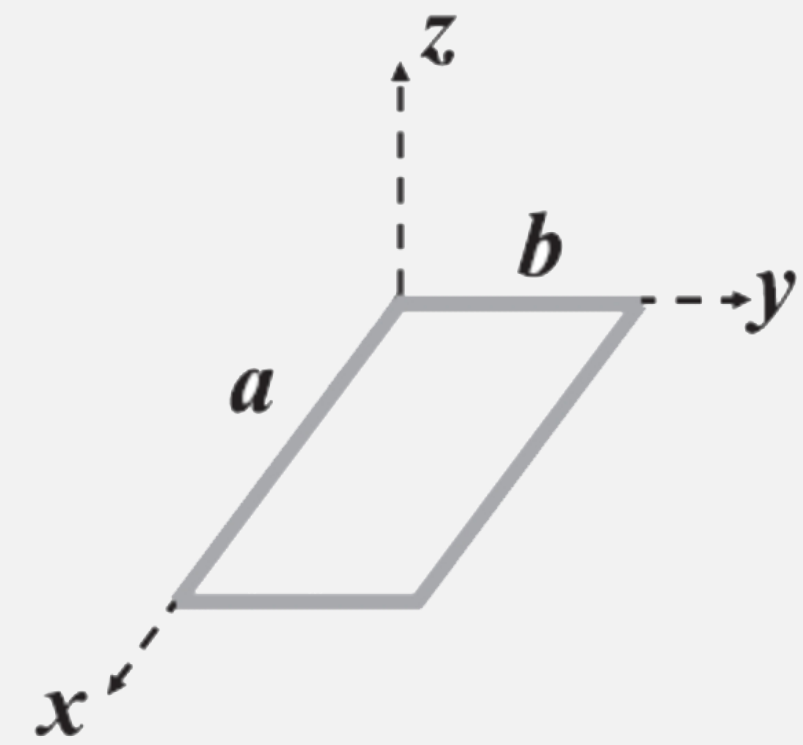 View Solution
View SolutionIn a region of space, the electric field is given by →E=8ˆi+4ˆj+3ˆk. The electric flux through a surface of area 100 units in the xy plane is
View SolutionA particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
View Solution

