A radioactive element X with half life 2 h decays giving a stable element Y. After a time t, ratio of X and Y atoms is 1:16 .Time t is
6 h
4 h
8 h
16 h
The correct Answer is:c
To solve the problem, we need to determine the time t when the ratio of the number of atoms of radioactive element X to the stable element Y is 1:16. We know that the half-life of element X is 2 hours.
1. Initial Setup:
- Let the initial number of atoms of element X be N0.
- Initially, the number of atoms of element Y is 0.
2. Decay After One Half-Life:
- After 2 hours (one half-life), the number of atoms of X will be:
NX=N02
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N02=N02
- The ratio NXNY is:
NXNY=N02N02=1:1
3. Decay After Two Half-Lives:
- After 4 hours (two half-lives), the number of atoms of X will be:
NX=N04
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N04=3N04
- The ratio NXNY is:
NXNY=N043N04=13(which is 1:3)
4. Decay After Three Half-Lives:
- After 6 hours (three half-lives), the number of atoms of X will be:
NX=N08
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N08=7N08
- The ratio NXNY is:
NXNY=N087N08=17(which is 1:7)
5. Decay After Four Half-Lives:
- After 8 hours (four half-lives), the number of atoms of X will be:
NX=N016
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N016=15N016
- The ratio NXNY is:
NXNY=N01615N016=115(which is 1:15)
6. Finding the Required Ratio:
- We need the ratio NXNY=116.
- This occurs after 8 hours, as we have established that after 8 hours the ratio is 1:15 and we can see that the next half-life would yield 1:16.
Conclusion:
The time t when the ratio of X to Y is 1:16 is 8 hours.
- Let the initial number of atoms of element X be N0.
- Initially, the number of atoms of element Y is 0.
- After 2 hours (one half-life), the number of atoms of X will be:
NX=N02
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N02=N02
- The ratio NXNY is:
NXNY=N02N02=1:1
- After 4 hours (two half-lives), the number of atoms of X will be:
NX=N04
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N04=3N04
- The ratio NXNY is:
NXNY=N043N04=13(which is 1:3)
- After 6 hours (three half-lives), the number of atoms of X will be:
NX=N08
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N08=7N08
- The ratio NXNY is:
NXNY=N087N08=17(which is 1:7)
- After 8 hours (four half-lives), the number of atoms of X will be:
NX=N016
- The number of atoms of Y formed will be:
NY=N0−NX=N0−N016=15N016
- The ratio NXNY is:
NXNY=N01615N016=115(which is 1:15)
- We need the ratio NXNY=116.
- This occurs after 8 hours, as we have established that after 8 hours the ratio is 1:15 and we can see that the next half-life would yield 1:16.
The time t when the ratio of X to Y is 1:16 is 8 hours.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - HOTS7videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - EXEMPLAR PROBLEMS7videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 350videos
PRACTICE PAPPER
Similar Questions
A radioactive element X decays to give two inert gasesX is
View SolutionA radioactive isotope X with half-life 1.5×109 yr decays into a stable nucleus Y .A rock sample contains both elements X and Y in the ratio 1 : 15. They age of the rock is
View SolutionA radioactive elementX converts into another stable elemnet Y. Half-life of X is 2h. Initally, only X is present. After time t, the ratio of atoms of X and Y is found to be 1:4 Then t in hours is .
View SolutionA radioactive nucleus A with a half life T, decays into nucleus B. At t=0, there is no nucleus B. At some time t, the ratio of the number of B to that of A is 0.3 . Then, t is given by
View SolutionA certain radioactive element has half-life of 4 days. The fraction of material that decays in 2days is
View SolutionA radioactiev nuleus X deays to a stable nuleus Y. Then, time graph of rate of formation of Y against time t will be:
View SolutionComplete the following table for a radioactive element whose half life is 5 minutes. Assume that you have 32 8 of this element at start, i.e., at t=0.
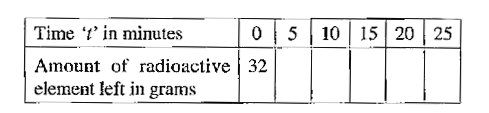
Now, using this data, plot the "decay curve"View SolutionA radio istoper X with a half-life 1.4×108 yr decays of Y which is stable. A sample of the rock from a cave was tound to contain X and Y in the ratio 1:7. The age of the rock is
View SolutionA radioactive isotope X with half-life of 693×109 years decay to Y which is stable. A sample of rock from of the moon was found to contain both the elements X Y in the mole ratio 1:7 . What is the age of the rock ?
View SolutionThe half-life of a radioactive isotope X is 50 yr. It decays to an other element Y which is stable. The two elements X and Y were found to be in the ratio of 1:15 in a sample of a give rock. The age of the rock was estimated to be
View Solution

