A vector is not changed if
It is displaced parallel to itself.
it is rotated through an arbitrary angle.
it is cross-multiplied by a unit vector.
it is multiplied by an arbitrary scalar.
The correct Answer is:A
To solve the question "A vector is not changed if," we need to analyze each of the provided options to determine which one does not alter the vector.
1. Understanding Vector Properties:
- A vector is defined by its magnitude and direction. Any operation that changes either of these will change the vector.
2. Analyzing Option 1: "Displaced parallel to itself"
- If a vector is displaced parallel to itself, it means it is moved without changing its direction or magnitude.
- Example: If vector A is moved from point (x1, y1) to (x1 + d, y1) while maintaining the same direction, it remains the same vector.
- Conclusion: This option does not change the vector.
3. Analyzing Option 2: "Rotated with an arbitrary angle"
- Rotating a vector changes its direction.
- Example: If vector A is rotated by 30 degrees, it points in a different direction.
- Conclusion: This option changes the vector.
4. Analyzing Option 3: "Cross multiplied by a unit vector"
- Cross multiplying a vector with a unit vector results in a new vector that is perpendicular to both original vectors.
- Example: If vector A is crossed with a unit vector k, the resulting vector is different in direction.
- Conclusion: This option changes the vector.
5. Analyzing Option 4: "Multiplied by an arbitrary scalar"
- Multiplying a vector by a scalar changes its magnitude.
- Example: If vector A is multiplied by 5, its magnitude increases, and it points in the same direction but is a different vector.
- Conclusion: This option changes the vector.
Final Conclusion:
The only option that does not change the vector is Option 1: "Displaced parallel to itself."
- A vector is defined by its magnitude and direction. Any operation that changes either of these will change the vector.
- If a vector is displaced parallel to itself, it means it is moved without changing its direction or magnitude.
- Example: If vector A is moved from point (x1, y1) to (x1 + d, y1) while maintaining the same direction, it remains the same vector.
- Conclusion: This option does not change the vector.
- Rotating a vector changes its direction.
- Example: If vector A is rotated by 30 degrees, it points in a different direction.
- Conclusion: This option changes the vector.
- Cross multiplying a vector with a unit vector results in a new vector that is perpendicular to both original vectors.
- Example: If vector A is crossed with a unit vector k, the resulting vector is different in direction.
- Conclusion: This option changes the vector.
- Multiplying a vector by a scalar changes its magnitude.
- Example: If vector A is multiplied by 5, its magnitude increases, and it points in the same direction but is a different vector.
- Conclusion: This option changes the vector.
The only option that does not change the vector is Option 1: "Displaced parallel to itself."
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS6videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS9videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
Similar Questions
(A): The direction of velocity vector remains unchanged though the coordinate system is changed
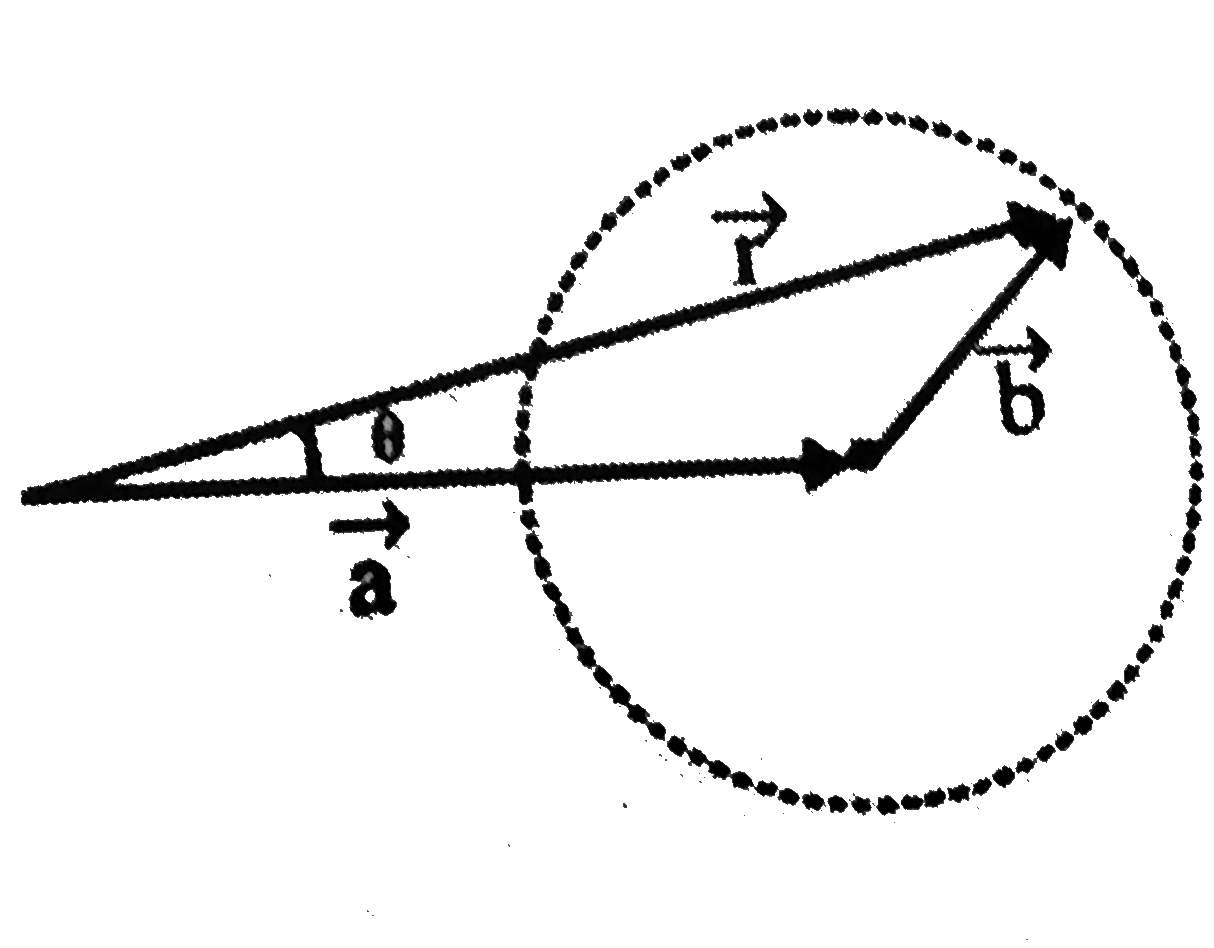
(R) : The direction of real vector is independent of coordinate systemView SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View Solution
Knowledge Check
- Question 1 - Select One
An impulse is supplied to a moving object with the force at an angle of 120∘ with respect to velocity vector. The angle between the impulse vector and the change in momentum vector is
A120∘B0∘C60∘D240∘
Asserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.View SolutionA vector may change when we :
View SolutionA vector may change when we :
View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View Solution