Suppose that two objects A and B are moving with velocities →vA and →vB (each with respect to some common frame of reference). Let →vAB represent the velocity of A with respect to B. Then
→vAB+→vBA=0
→vAB−→vBA=0
→vAB=→vA+→vB
|→vAB|≠|→vBA|
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the velocities of two objects A and B, and their relative velocities.
1. Define the Velocities:
Let →vA be the velocity of object A and →vB be the velocity of object B, both with respect to a common frame of reference.
2. Relative Velocity Definition:
The velocity of A with respect to B, denoted as →vAB, can be defined as:
→vAB=→vA−→vB
3. Velocity of B with respect to A:
Similarly, the velocity of B with respect to A, denoted as →vBA, can be defined as:
→vBA=→vB−→vA
4. Relate →vAB and →vBA:
We can express →vBA in terms of →vAB:
→vBA=−(→vAB)
5. Magnitude Relationship:
From the above relationship, we see that:
|→vBA|=|→vAB|
This means the magnitudes of the velocities of A with respect to B and B with respect to A are equal.
6. Evaluate Options:
- Option 1: →vAB+→vBA=0 is correct because →vBA=−→vAB.
- Option 2: →vAB−→vBA=0 is incorrect because →vAB−(−→vAB)=2→vAB≠0.
- Option 3: →vAB=→vA+→vB is incorrect as shown in the definitions.
- Option 4: The magnitudes are equal, so this option is incorrect as it states they are not equal.
7. Conclusion:
The only correct statement is that the velocity of A with respect to B plus the velocity of B with respect to A equals zero.
Final Answer:
The correct option is:
→vAB+→vBA=0
Let →vA be the velocity of object A and →vB be the velocity of object B, both with respect to a common frame of reference.
The velocity of A with respect to B, denoted as →vAB, can be defined as:
→vAB=→vA−→vB
Similarly, the velocity of B with respect to A, denoted as →vBA, can be defined as:
→vBA=→vB−→vA
We can express →vBA in terms of →vAB:
→vBA=−(→vAB)
From the above relationship, we see that:
|→vBA|=|→vAB|
This means the magnitudes of the velocities of A with respect to B and B with respect to A are equal.
- Option 1: →vAB+→vBA=0 is correct because →vBA=−→vAB.
- Option 2: →vAB−→vBA=0 is incorrect because →vAB−(−→vAB)=2→vAB≠0.
- Option 3: →vAB=→vA+→vB is incorrect as shown in the definitions.
- Option 4: The magnitudes are equal, so this option is incorrect as it states they are not equal.
The only correct statement is that the velocity of A with respect to B plus the velocity of B with respect to A equals zero.
The correct option is:
→vAB+→vBA=0
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS
6 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS
9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
Two objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionSTATEMENT -1 : For an observer looking out through the window of a fast moving train , the nearby objects appear to move in the opposite direction to the train , while the distant objects appear to be stationary .
STATEMENT - 2 : If the observer and the object are moving at velocities →v1 and →v2 respecttively with refrence to a laboratory frame , the velocity of the object with respect to a laboratory frame , the velocity of the object with respect to the observer is →v2−→v(1) .
(a) Statement -1 is True, statement -2 is true , statement -2 is a correct explanation for statement -1
(b) Statement 1 is True , Statement -2 is True , statement -2 is NOT a correct explanation for statement -1
(c) Statement - 1 is True , Statement -2 is False
(d) Statement -1 is False, Statement -2 is True
View SolutionSTATEMENT -1 : For an observer looking out through the window of a fast moving train , the nearby objects appear to move in the opposite direction to the train , while the distant objects appear to be stationary .
STATEMENT - 2 : If the observer and the object are moving at velocities →v1 and →v2 respecttively with refrence to a laboratory frame , the velocity of the object with respect to a laboratory frame , the velocity of the object with respect to the observer is →v2−→v(1) .
(a) Statement -1 is True, statement -2 is true , statement -2 is a correct explanation for statement -1
(b) Statement 1 is True , Statement -2 is True , statement -2 is NOT a correct explanation for statement -1
(c) Statement - 1 is True , Statement -2 is False
(d) Statement -1 is False, Statement -2 is True
View SolutionTwo objects A and B are moving with velocities vAandvB respectively along positive x-axis. If vA<vB then, which of the following position-time graphs is correctly showing the velocity of A and B ?
View SolutionWrite the vector representation of the vectors A and B with respect to the frame of reference shown in the figure.

View SolutionConsdier the situation shown in figure
(I ) find out velocity of B with respect to A
(ii ) Find out velocity of A with respect to B

View SolutionAssertion : An object has given two velocities →v1 and →v2 has a resultant velocity →v=→v1+→v2.
Reason : →v1and→v2 should be velocities with reference to some common reference frame.
View SolutionTwo object A and B are moving each with velocities 10 m/s. A is moving towards East and B is moving towards North from the same point as shown. Find velocity of A relative to B (→VAB)
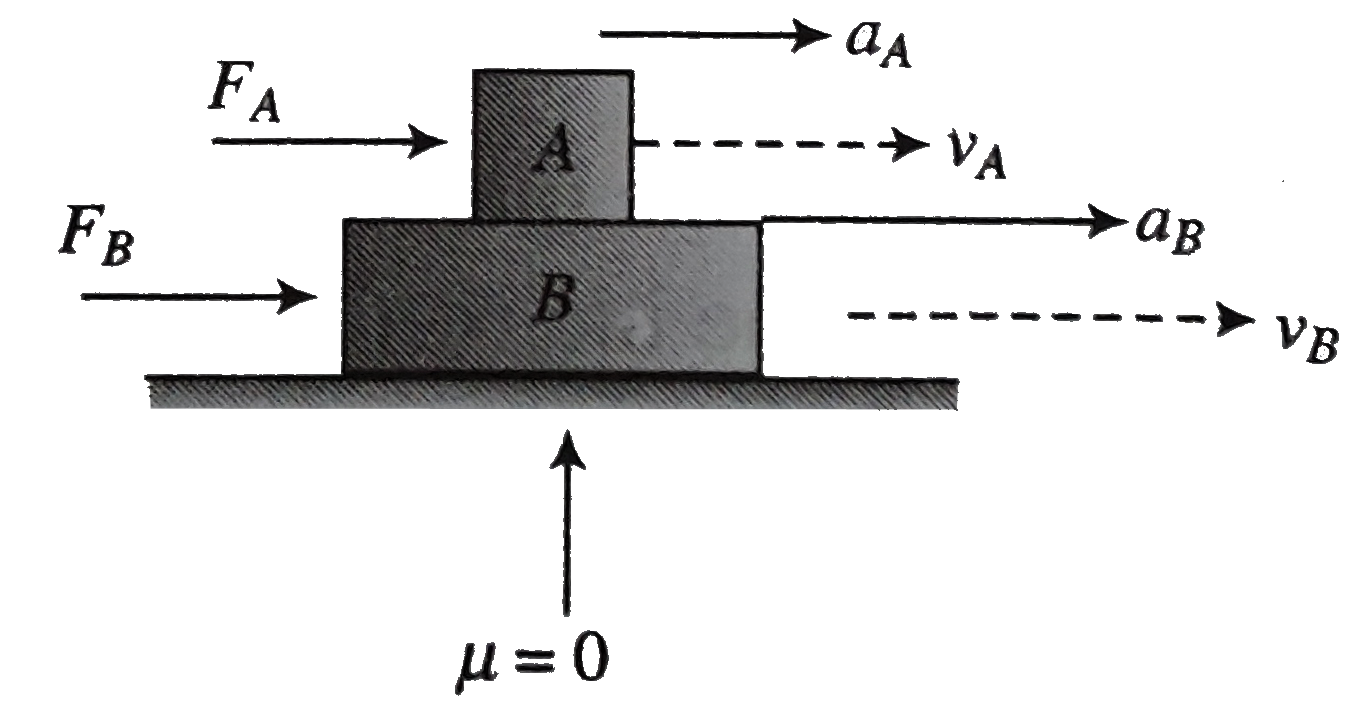
View SolutionTwo rough blocks A and B ,A placed over B move with acceleration →aA and →aB veclocities →v(A) and →vB by the action of horizontal forces −→FA and −→FB, respectively. When no friction exsits between the blocks A and B,
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
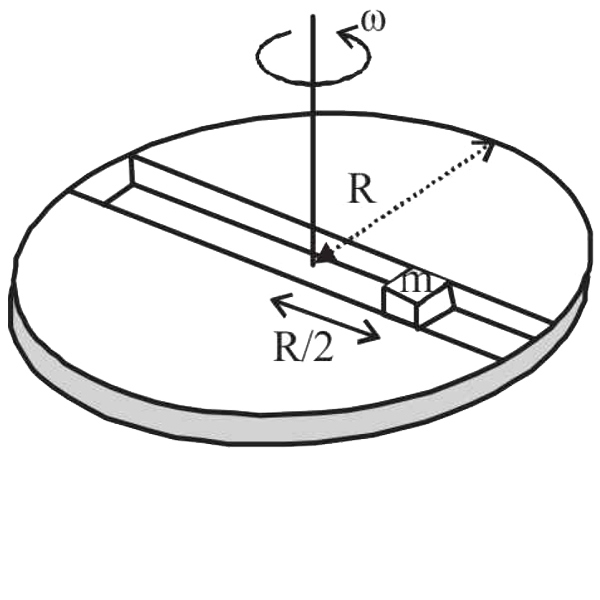
The distance r of the block at time is
View Solution
