What is approximately the centripetal acceleration (in units of acceleration due to gravity on earth, g = 10 m s−2 of an air-craft flying at a speed of 400 m s−1 through a circular arc of radius 0.6 km ?
26.7
16.9
13.5
30.2
The correct Answer is:A
To find the centripetal acceleration of the aircraft flying through a circular arc, we can follow these steps:
Step 1: Identify the given values
- Speed of the aircraft (V) = 400 m/s
- Radius of the circular arc (R) = 0.6 km = 0.6 × 10^3 m = 600 m
Step 2: Use the formula for centripetal acceleration
The formula for centripetal acceleration (a_c) is given by:
ac=V2R
Step 3: Substitute the values into the formula
Now, substitute the values of V and R into the formula:
ac=(400m/s)2600m
Step 4: Calculate V^2
Calculate V2:
V2=4002=160000m2/s2
Step 5: Calculate centripetal acceleration
Now substitute V2 into the centripetal acceleration formula:
ac=160000m2/s2600m
Step 6: Perform the division
Now perform the division:
ac=160000600≈266.67m/s2
Step 7: Convert to units of g
To express this in terms of acceleration due to gravity (g = 10 m/s²):
Centripetal acceleration in terms of g=266.67m/s210m/s2≈26.67g
Final Answer
Thus, the centripetal acceleration of the aircraft is approximately 26.7 g.
---
- Speed of the aircraft (V) = 400 m/s
- Radius of the circular arc (R) = 0.6 km = 0.6 × 10^3 m = 600 m
The formula for centripetal acceleration (a_c) is given by:
ac=V2R
Now, substitute the values of V and R into the formula:
ac=(400m/s)2600m
Calculate V2:
V2=4002=160000m2/s2
Now substitute V2 into the centripetal acceleration formula:
ac=160000m2/s2600m
Now perform the division:
ac=160000600≈266.67m/s2
To express this in terms of acceleration due to gravity (g = 10 m/s²):
Centripetal acceleration in terms of g=266.67m/s210m/s2≈26.67g
Thus, the centripetal acceleration of the aircraft is approximately 26.7 g.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - HOTS
6 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXEMPLER PROBLEMS
9 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
The acceleration due to gravity is 9.8ms−2. Give its value in ft s−2
View SolutionSuppose the acceleration due to gravity at a place is 10ms2. Find its value in cm//(minute).
View SolutionIf the acceleration due to gravity on earth is 9.81m/s2 and the radius of the earth is 6370 km find the mass of the earth ?
(G=6.67×10−11Nm2/kg2)
View SolutionIf the radius of the earth be 6.38x104m and the acceleration due to gravity at earth be 9.8ms∧(2) then calculate the escape velocity of a body from the earth.s surface.
View SolutionThe acceleration due to gravity at the moon's surface is 1.67ms−2. If the radius of the moon is 1.74×106m, calculate the mass of the moon.
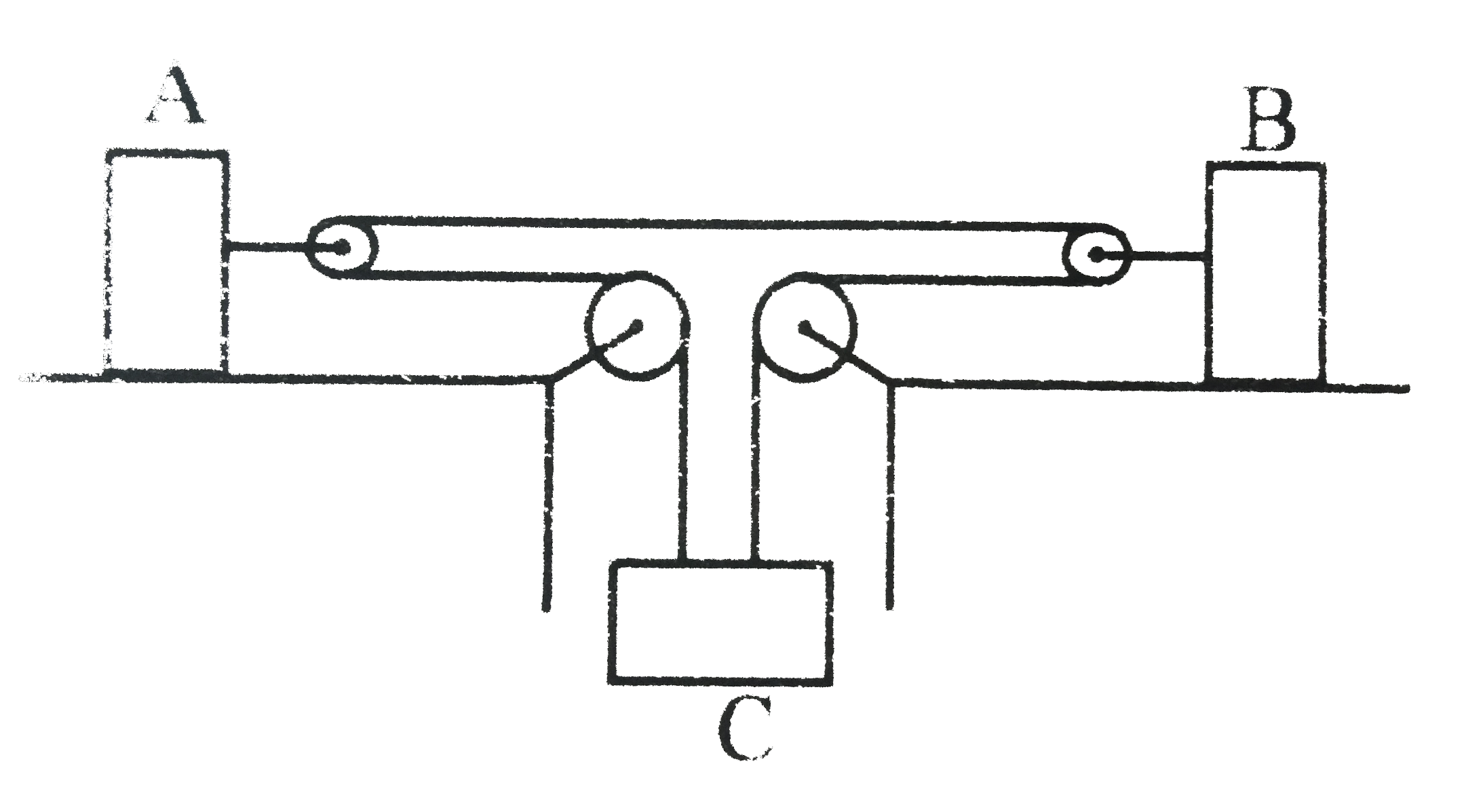
View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
View SolutionWhat is the value of acceleration due to gravity at a height equal to half the radius of earth, from surface of earth ? [take g=10m/s2 on earth's surface]
View SolutionAcceleration due to gravity at earth's surface is 10m−2 The value of acceleration due to gravity at the surface of a planet of mass 12 th and radius 12 of f the earth is -
View SolutionCentripetal acceleration of a cyclist completing 7 rounds in a minute along a circular track of radius 5 m with a constant speed ,is
View SolutionThe weight of a body on earth is 98 N where the acceleration due to gravity is 9.8 ms−2. What will be its mass .
View Solution
