Figure shows the displacement-time graphs of two simple harmonic motions I and II. From the graph it follows that

curve I has samme frequency as that of curve II.
curve I has frequency twice that of curve II.
curve I has frequency half that of curve II
curve I has frequency four times that of curve II.
The correct Answer is:C

From the graph
for curve I,
time period, T1=8s, frequency υ1=1T1=18Hz
For curve II,
Time period, T2=4s, frequency, υ2=1T2=14Hz
Their corresponding ratio
υ1υ2=12 or υ1=12υ2.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills8videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems9videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason10videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
The time period of simple harmonic motion depends upon
AamplitudeBenergyCphase constantDmass
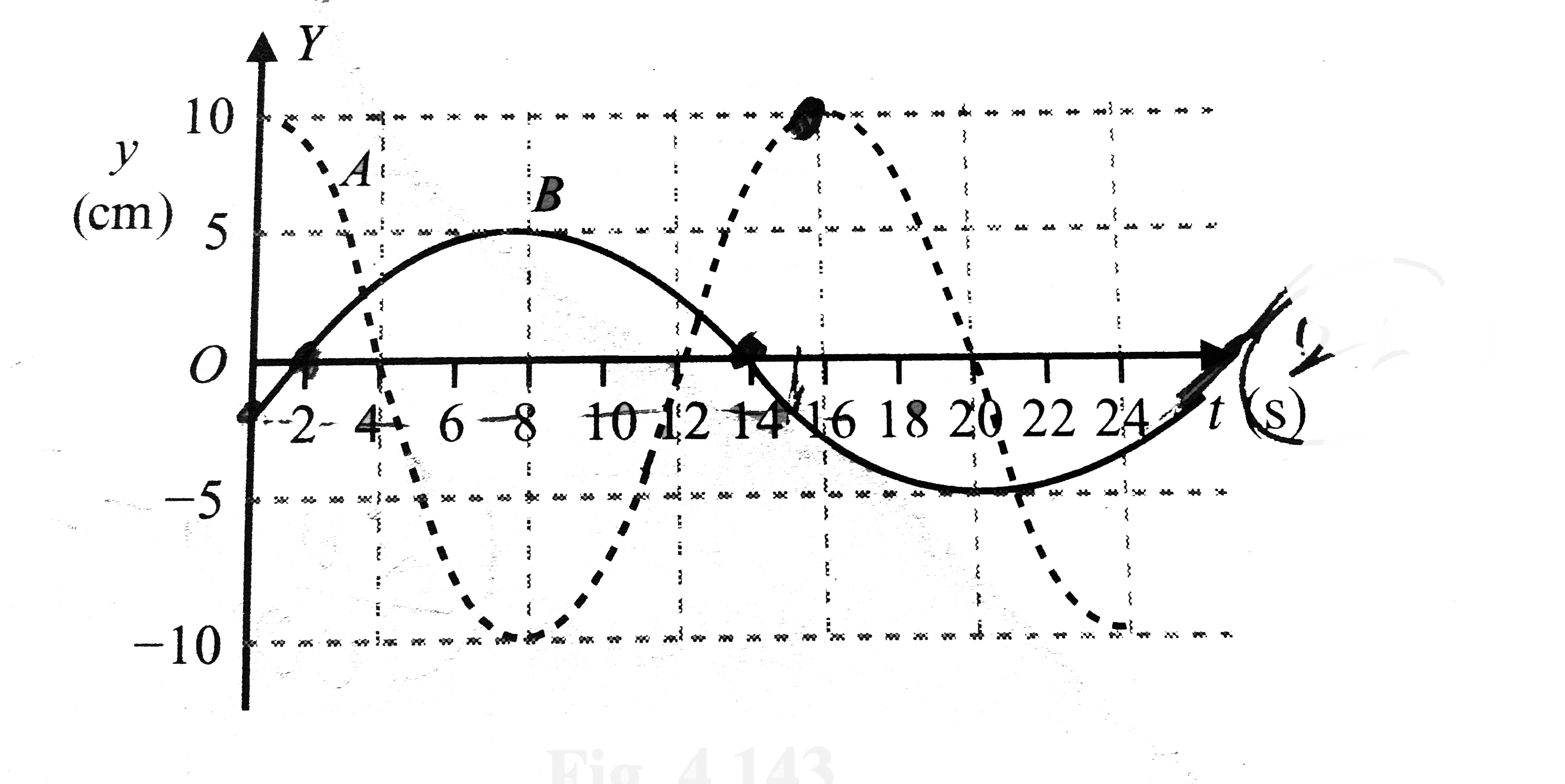
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities isView SolutionFigures (i) and (ii) below show the displacement - time graphs of two particles moving along the x-axis. We can say that
 View Solution
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
View SolutionFigure given shows the distance - time graph of the motion of a car. It follows from the graph that the car is
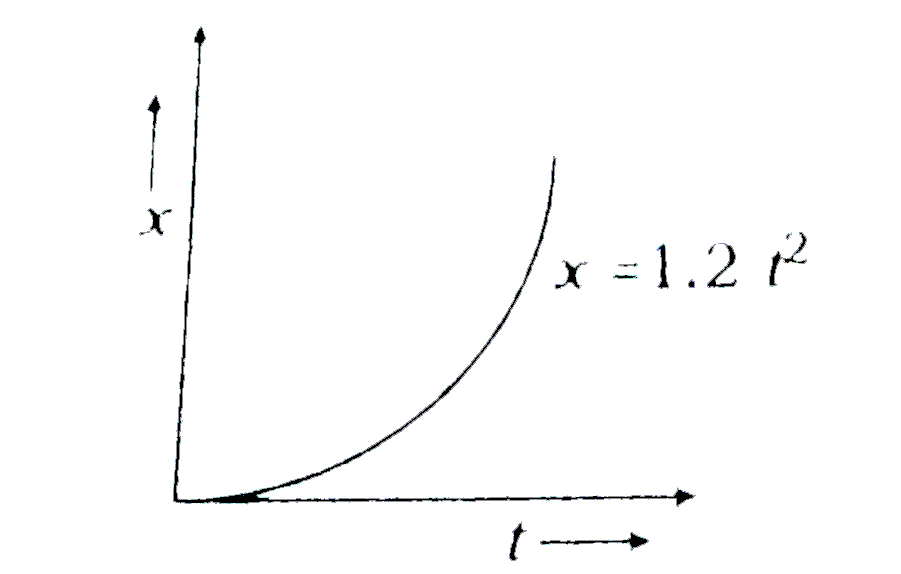 View Solution
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
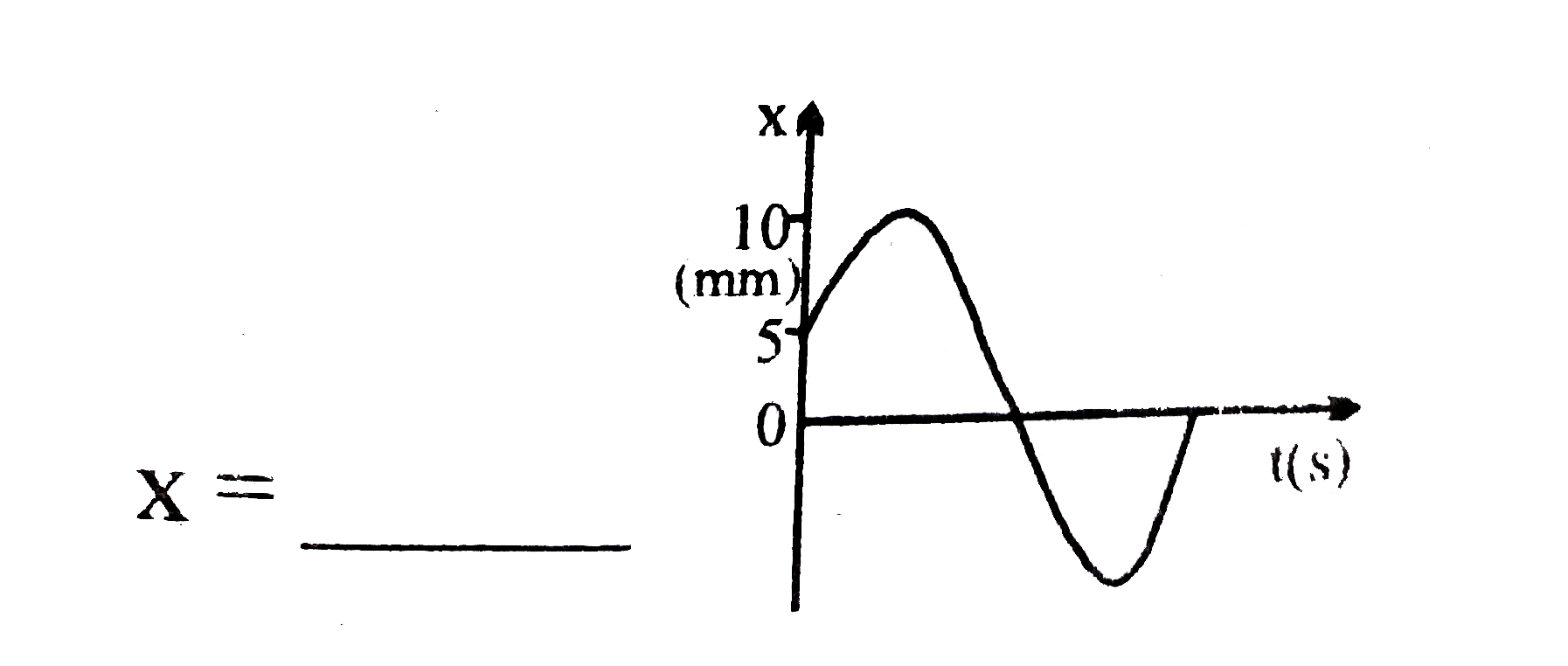 View Solution
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
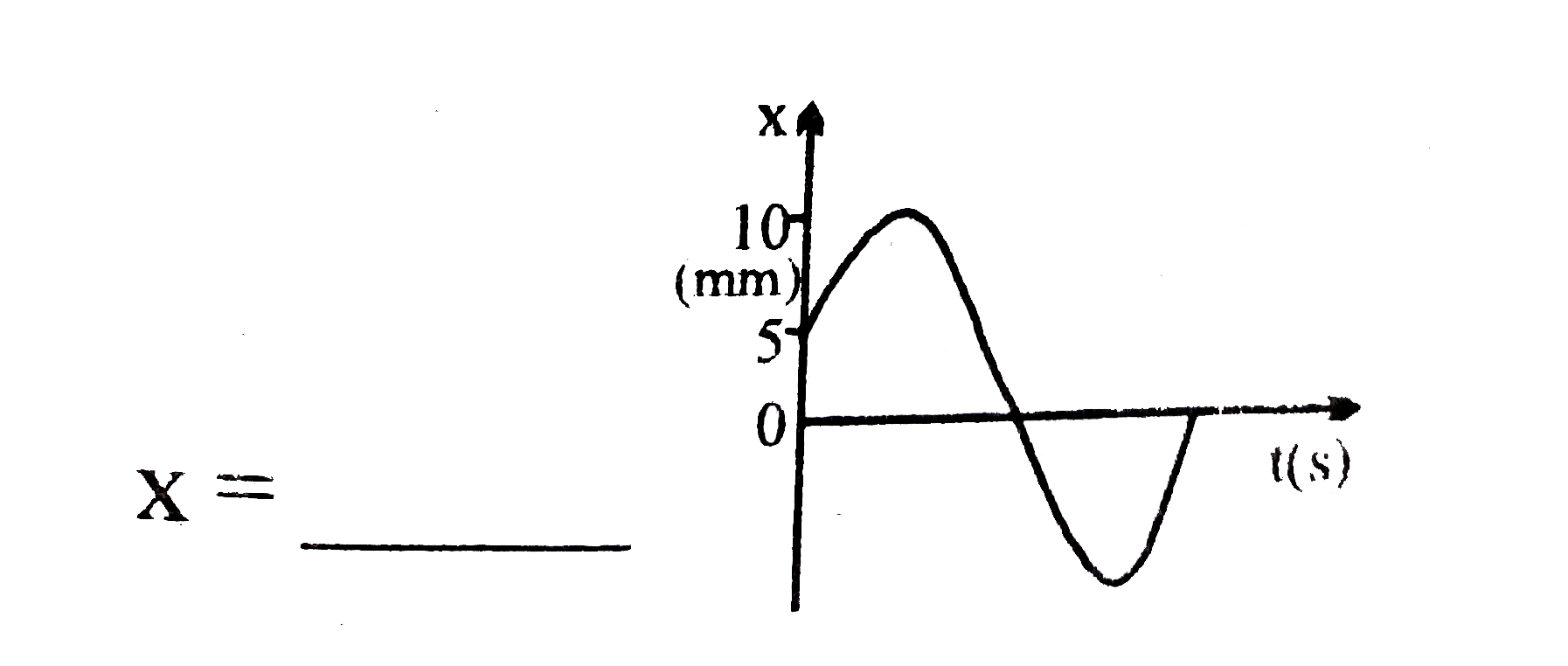 View Solution
View SolutionFigure shows the stress-strain graphs for materials .A and B. From the graph it follows that
 View Solution
View Solution


