An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
12π√MV0AγP0
12πAγP0V0M
12πV0MP0A2γ
12π√A2γP0MV0
The correct Answer is:D
To solve the problem of the piston executing simple harmonic motion in an ideal gas, we can follow these steps:
Step 1: Understand the equilibrium condition
At equilibrium, the forces acting on the piston are balanced. The pressure force exerted by the gas inside the cylinder must balance the weight of the piston and the atmospheric pressure acting on the piston.
Equation at equilibrium:
P0A=mg+PatmA
Step 2: Displace the piston
When the piston is displaced by a small distance x from its equilibrium position, the pressure inside the gas changes. The new pressure can be expressed as:
P=P0+ΔP
where ΔP is the change in pressure due to the displacement.
Step 3: Apply the adiabatic condition
Since the system is isolated, the process is adiabatic. For an adiabatic process, we use the relation:
PVγ=constant
Differentiating this gives:
PdV+VdP=0
From this, we can express dP:
dP=−PVdV
Step 4: Relate volume change to displacement
The volume change dV due to the displacement x of the piston can be expressed as:
dV=Adx
Substituting this into the expression for dP:
dP=−P0V0Adx
Step 5: Set up the equation of motion
Now, we can set up the equation of motion for the piston. The net force acting on the piston when displaced is:
Fnet=PA−PatmA−mg
Substituting the expressions we have:
(P0+dP)A−PatmA−mg=ma
Substituting dP:
(P0−P0AV0x)A−PatmA−mg=ma
Step 6: Simplify the equation
After substituting and simplifying, we find that:
−P0A2V0x=ma
This implies:
a=−P0A2mV0x
Step 7: Identify the form of SHM
The equation a=−ω2x indicates simple harmonic motion, where:
ω2=P0A2mV0
Step 8: Calculate the frequency
The frequency f of the oscillation is given by:
f=ω2π=12π√P0A2mV0
Final Result
Thus, the frequency of the simple harmonic motion of the piston is:
f=12π√γP0A2mV0
At equilibrium, the forces acting on the piston are balanced. The pressure force exerted by the gas inside the cylinder must balance the weight of the piston and the atmospheric pressure acting on the piston.
P0A=mg+PatmA
When the piston is displaced by a small distance x from its equilibrium position, the pressure inside the gas changes. The new pressure can be expressed as:
P=P0+ΔP
where ΔP is the change in pressure due to the displacement.
Since the system is isolated, the process is adiabatic. For an adiabatic process, we use the relation:
PVγ=constant
Differentiating this gives:
PdV+VdP=0
From this, we can express dP:
dP=−PVdV
The volume change dV due to the displacement x of the piston can be expressed as:
dV=Adx
Substituting this into the expression for dP:
dP=−P0V0Adx
Now, we can set up the equation of motion for the piston. The net force acting on the piston when displaced is:
Fnet=PA−PatmA−mg
Substituting the expressions we have:
(P0+dP)A−PatmA−mg=ma
Substituting dP:
(P0−P0AV0x)A−PatmA−mg=ma
After substituting and simplifying, we find that:
−P0A2V0x=ma
This implies:
a=−P0A2mV0x
The equation a=−ω2x indicates simple harmonic motion, where:
ω2=P0A2mV0
The frequency f of the oscillation is given by:
f=ω2π=12π√P0A2mV0
Thus, the frequency of the simple harmonic motion of the piston is:
f=12π√γP0A2mV0
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion & Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
An ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionAn ideal gas enclosed in a cylinder fitted with a frictionless and weightless piston, pushes it outside. What would be the sign convention for the work ?
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
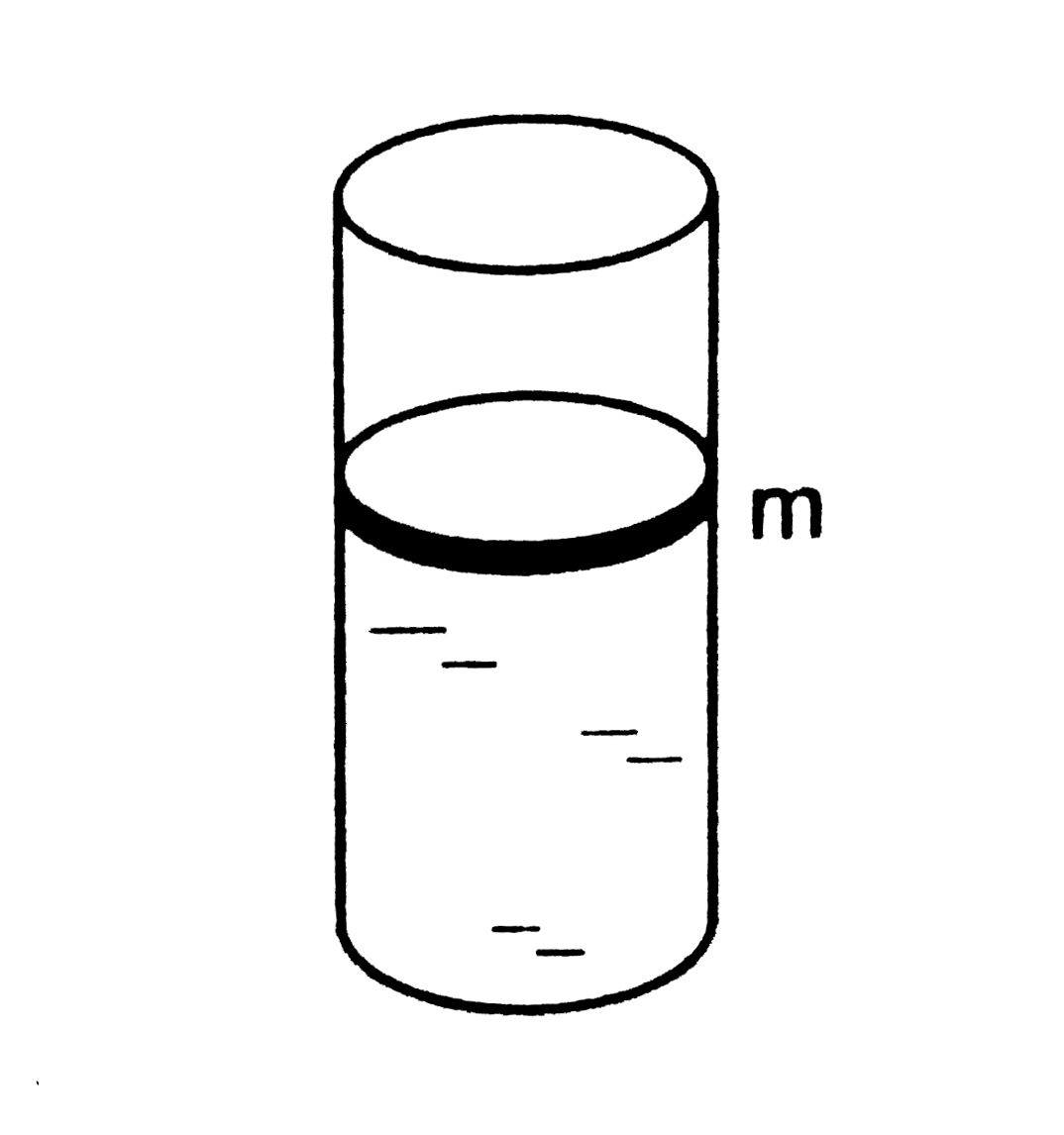 ,
,
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P0. Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.

View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
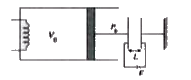
View SolutionMethod 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.

View SolutionAn ideal monoatomic gas is enclosed in a fixed horizontal adiabatic cylinder of cross sectional area A. The cylinder is fitted with an adiabatic piston of mass m (attached to one end of a spring as shown) which can move horizontally without friction inside the cylinder. In equilibrium, the spring is in natural length and pressure and volume are P0 and V0 respectively. The piston is slightly displaced from equilibrium and released. Then, frequency of small oscillation is

View Solutionshows a cylindrical tube of cross-sectional area A fitted with two frictionless pistons. The pistons are connected to each other by a metallic wire. Initially, the temperature of the gas is T0and its pressure is p0which equals the atmospheric pressure, (a)What is the tention in the wire?(b)What will be the tention if the temperature is increased to 2T_(0)?

View SolutionAn ideal gas is enclosed in a cyclinder with a movable piston on top. The piston has mass of 8000g and an area of 5.00cm2 and is free to slide up and down, keeping the pressure of the gas constant. How much work is done as the temperature of 0.200mol of the gas is raised from 200∘C to 300∘C?
View Solution
