A smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P0. Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.

The correct Answer is:√γP0A2mV0
In adabatic procedure, PVγ=C
Taking log of sides, we have logP+γlogV=logC
Taking difference of both sides, we have δPP+γδVV=0
This gives the excess presure ΔP (where we disturb the position) as
δP=−γPVδV
where ΔV=charge in valume of the gas=AΔx
Substituting δP=δFA,V=V0.p=p0andδV=Aδx
We have keff=[δfδx]=γP0A2V0
Then, using ω=√keffm
We have ω=√γP0A2mV0
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single Correct
Explore 107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.2
Explore 23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View Solution
Knowledge Check
An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A12π√MV0AγP0B12πAγP0V0MC12πV0MP0A2γD12π√A2γP0MV0
A movable piston separates a sample of gas from vacuum. In this state, pressure of gas is P, then find pressure after piston is released
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionFollowing figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P1 and temperature T1 in left part and gas at pressure P2 and temperature T2 in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

View Solution
A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is P0 and temperature is T0, atmospheric pressure is also P0. Now the temperature of the gas is increased to 2T0, the tension in the wire will be
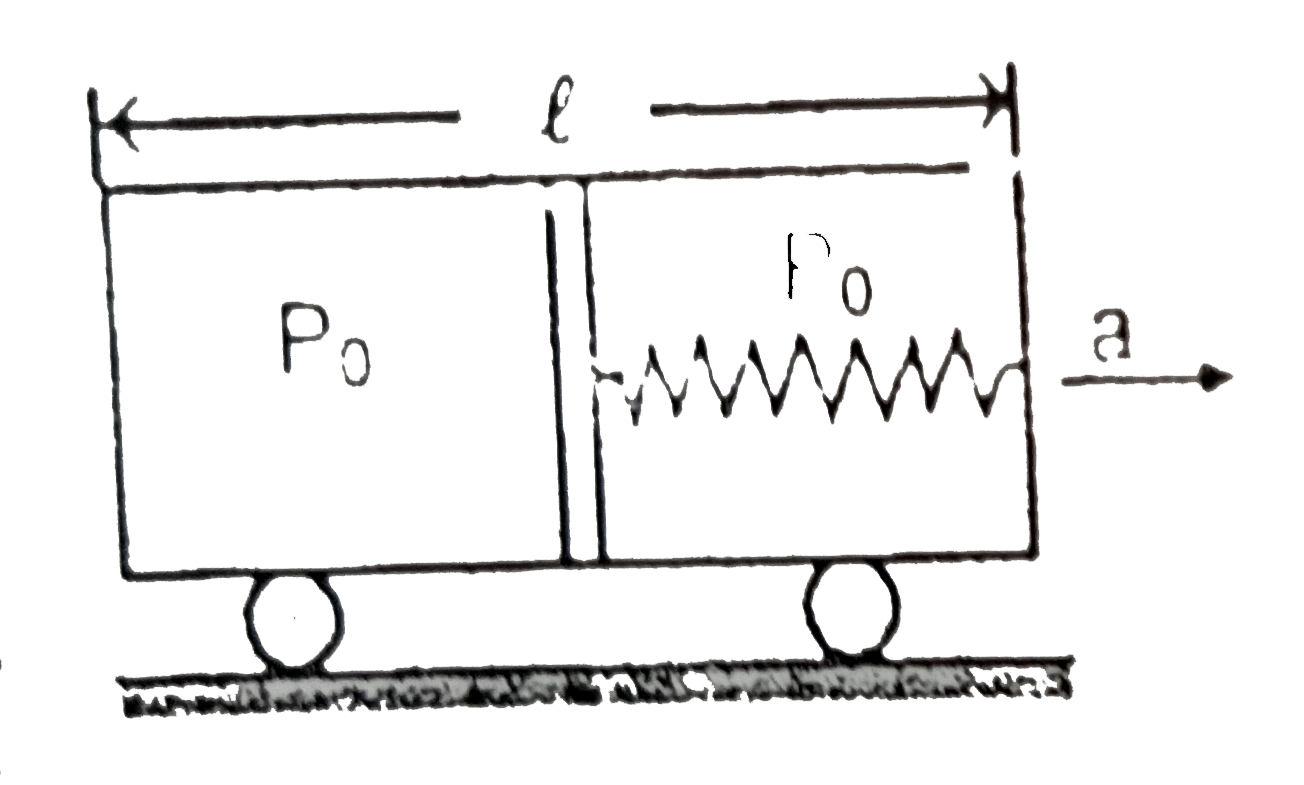
View SolutionAn adiabatic piston of mass m equally divides an insulated container of total volume v0 and length l. A light spring connect the piston to right wall. The container has helium gas. The pressure on both side of piston is P0. The container starts moving with acceleration 'a' towards right, find the stretch of the spring when acceleration of the piston equals acceleration of container. (Assume displacement of the piston <<l)
View Solution
