The X-z plane separates two media A and B of refractive indicesμ1=1.5andμ2=2.A ray of light travels from A to B. Its directions in the two media are given by unit vectors ¯u1=aˆi+bˆjand¯u2=cˆi+dˆj. Then
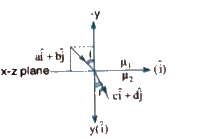
tani=absosinIa√a2+b2
andtanr=Cd,sinr=c√c2+d2
μ1sinI=μ2sinr
(32)(a√a2+b2)=2(c√c2+d2)
But as aˆi+bˆjandcˆi+dˆj are unit vectors so
√a2+b2=√c2+d2=1
hence 32a=2c,soac=43
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
37 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
50 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
6 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - II
31 Videos
Similar Questions
The x-z plane separates two media A and B of refractive indices μ1=1.5 and μ2=2. A ray of light travels from A to B. Its directions in the two media are given by unit vectors u1=aˆi+bˆj and u2=cˆi+aˆj. Then
View SolutionThe xz plane separates two media A and B with refractive indices μ1 & μ2 respectively. A ray of light travels from A to B. Its directions in the two media are given by the unit vectors, →rA=aˆi+bˆj & →rB=αˆi+βˆj respectively where ˆi & ˆj are unit vectors in the x & y directions. Then :
View Solution
Knowledge Check
The x-z plane separates two media A and B of refractive indices μ1=1.5 and μ2=2. A ray of light travels from A to B. Its directions in the two media are given by unit vectors u1=aˆi+bˆj and u2=cˆi+aˆj. Then
Aac=43Bac=34Cbc=43Dbd=34The xz plane separates two media A and B with refractive indices μ1 & μ2 respectively. A ray of light travels from A to B. Its directions in the two media are given by the unut vectors, →rA=aˆi+bˆj & →rBαˆi+βˆj respectively where ˆi & ˆj are unit vectors in the x & y directions. Then :
Aμ1a=μ2αBμ1α=μ2aCμ1bμ2βDμ1β=μ2bTwo thin slabs of refractive indicies μ1 and μ2 are placed parllel to each other in the x−z plane. If the direction of propagation of a ray in the two media are along the vectors →r1=aˆi+bˆj and →r2=cˆi+dˆj and ˆn is unit vector along the common normal of the slabs, then we have
 Aμ1b√a2+b2=μ2d√c2+d2Bμ1a√a2+b2=μ2c√c2+d2C→r1⋅(ˆn×→r2)=0D→r1×(ˆn×→r2)=0
Aμ1b√a2+b2=μ2d√c2+d2Bμ1a√a2+b2=μ2c√c2+d2C→r1⋅(ˆn×→r2)=0D→r1×(ˆn×→r2)=0
The xz plane separates two media A and B with refractive indices μ1 & μ2 respectively. A ray of light travels from A to B. Its directions in the two media are given by the unut vectors, →rA=aˆi+bˆj & →rBαˆi+βˆj respectively where ˆi & ˆj are unit vectors in the x & y directions. Then :
View SolutionTwo thin slabs of refractive indices μ1 and μ2 are placed parallel to each other in the x-z plane. If the direction of propagation of a ray in the two media are along the vectors →r1=aˆi+bˆj and →r2=cˆi+dˆj then we have:

View SolutionTwo thin slabs of refractive indices μ1 and μ2 are placed parallel to each other in the x-z plane. If the direction of propagation of a ray in the two media are along the vectors →r1=aˆi+bˆj and →r2=cˆi+dˆj then we have:

View SolutionTwo thin slabs of refractive indices μ1 and μ2 are placed parallel to each other in the x-z plane. If the direction of propagation of a ray in the two media are along the vectors →r1=aˆi+bˆj and →r2=cˆi+dˆj then we have:

View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
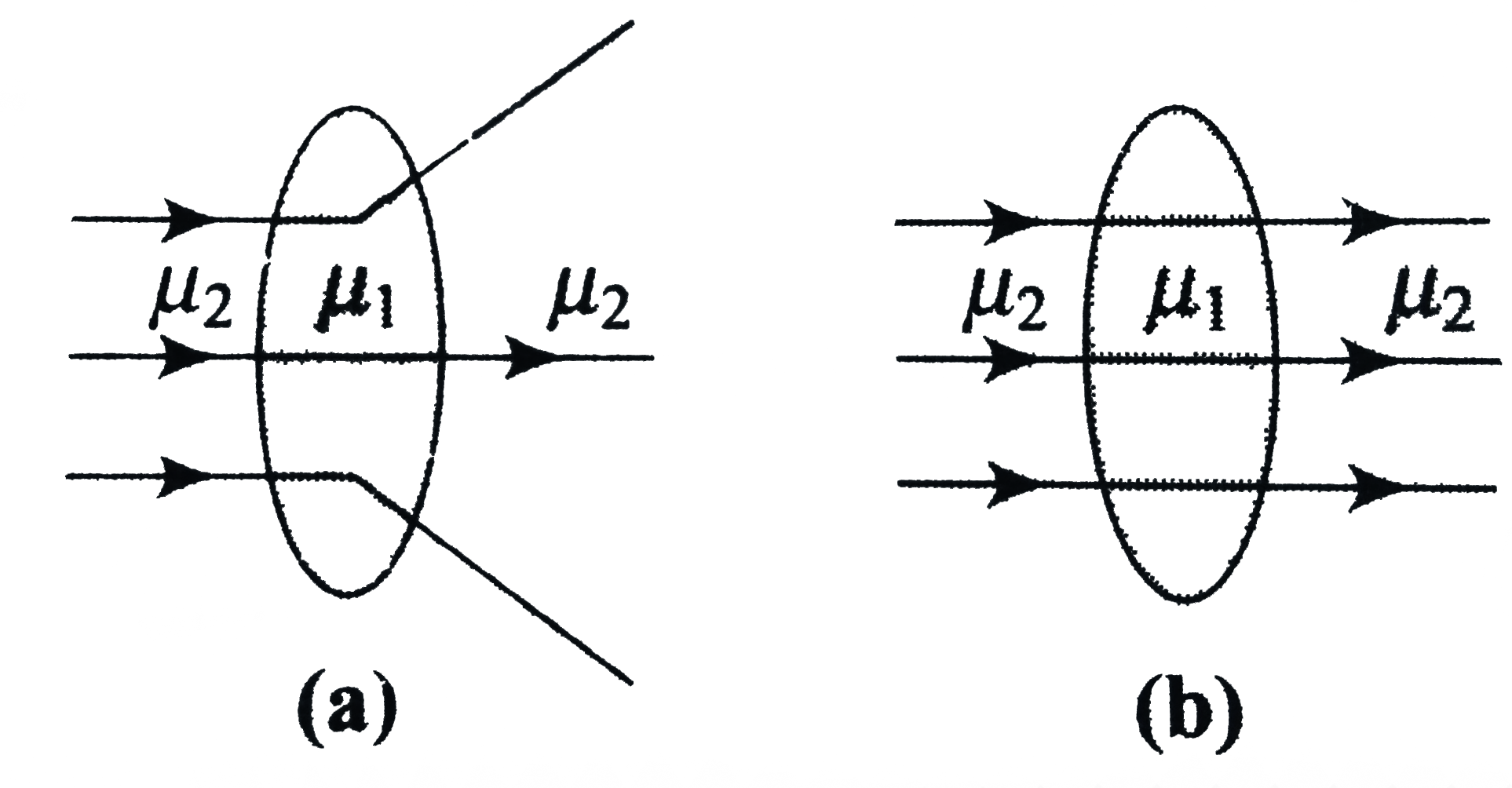
View Solution
