A solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflections have taken place.
The ray of light first gets refracted then reflected and then again rcfracted. For first refraction and then reflection the ray of light travels from left to right while for the last refraction it travels from right to left. Hence, the sign convention will change accordingly.
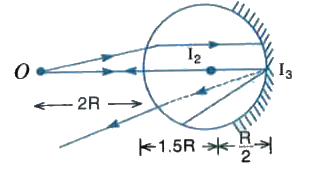
First : refraction
Using μ2vμ1u=μ2−μ1R with proper sign convertions ,
we have 1.5v−1.0−2R=1.5−1.0+R∴v1=∞
Second : reflection
Using 1v+1u=1f=2R with proper sign conventions
we have 1v2+1∞=−2R
∴V2=−R2
Third: refraction
Again using μ2v−μ1u=μ2−μ1R with reversed sign convention , we have 1.0v3−1.5−1.5R=1.0−1.5−R
orV3=−2R i.e., final image is formed on the vertex of the silvered face
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
37 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
50 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
6 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - II
31 Videos
Similar Questions
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.
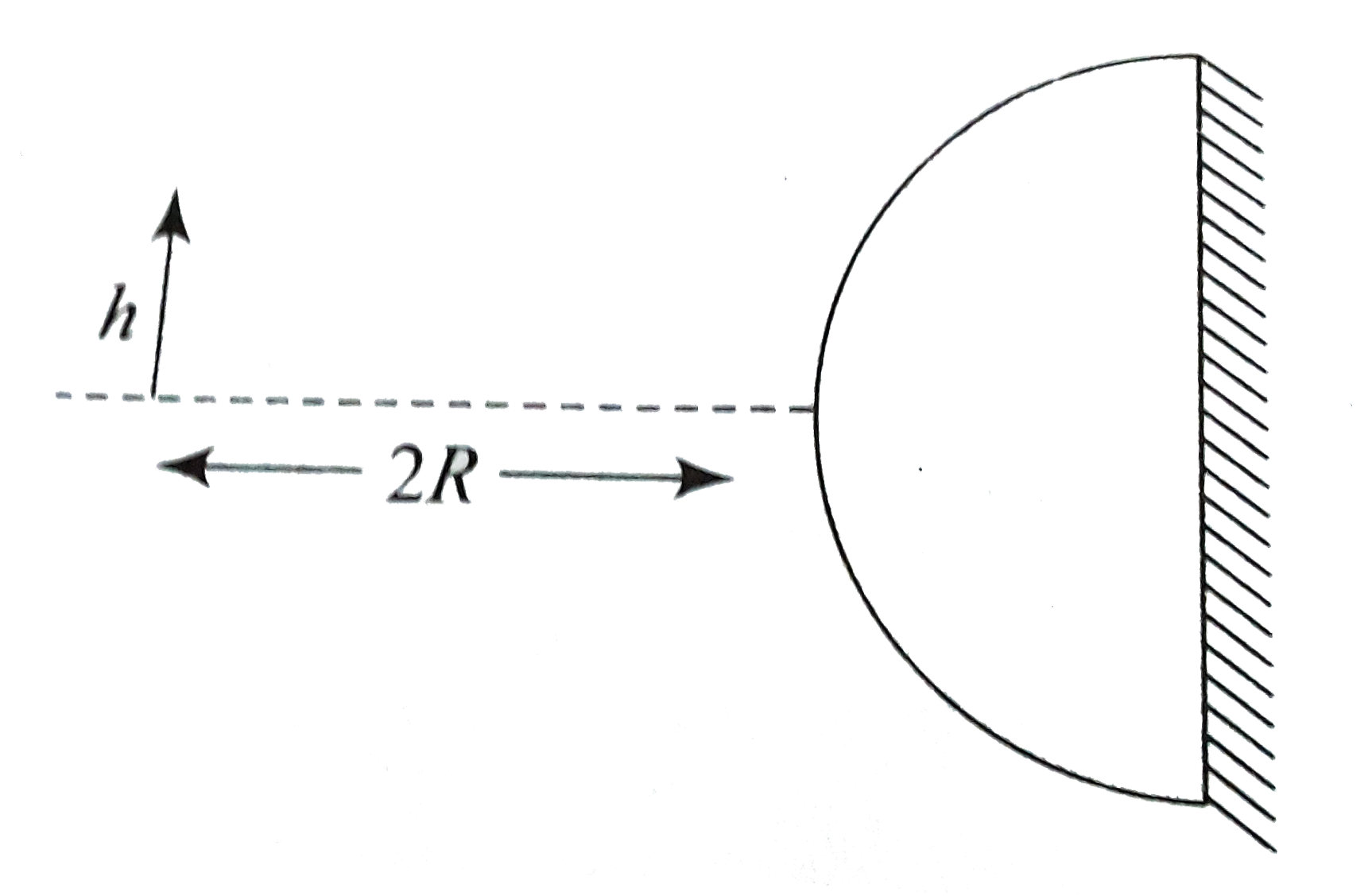
View SolutionA hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View Solution
Knowledge Check
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.
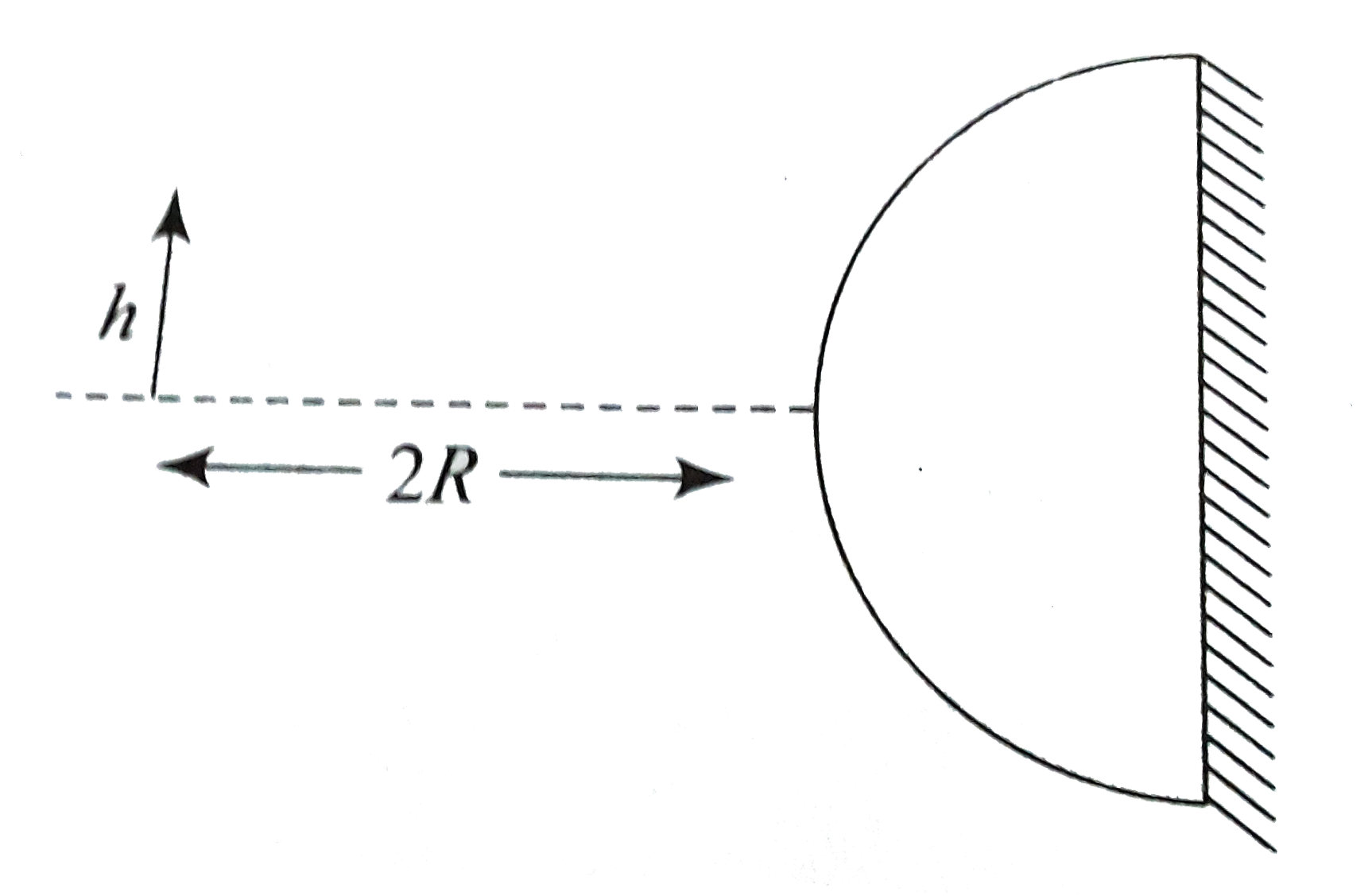 Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left side
Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left sideA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
A24 cm from the surfaceB36 cm from the centreC24 cm from the centreDBoth (1) & (2)There is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
ARμ−1BRμCR2−μD2Rμ−1
A hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View SolutionA hemisphere of radius R, made of glass of refractive index (3/2) is placed on 'the table. A point source of light is placed at a distance 2R from the centre, of hemisphere. If source is viewed diametrically opposite side of hemisphere. Find the position of image of source.

View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ1.5.
View SolutionFigure shows a glass hemisphere M of μ=32 and radius 10 cm. a point object O is placed at a distance 20 cm behind the flat face which is viewed by an observer from the curved side. Find location of final image after two refractions as seen by observer.
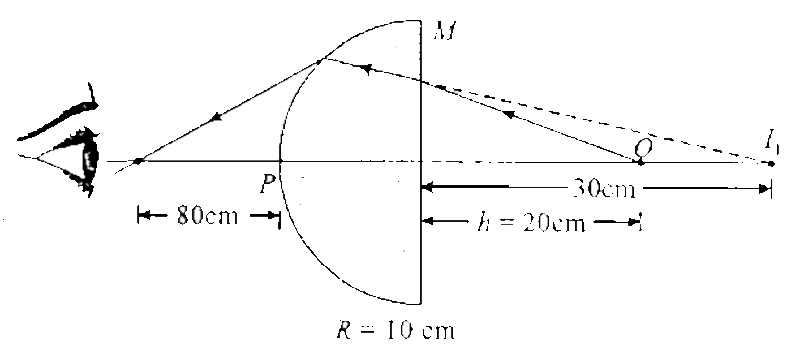
View Solution
