A particle is projected horizontally with a speed u from the top of plane inclined at an angle $θ$ with the horizontal. How far from the point of projection will particle strike the plane?

Text Solution

Verified by Experts

Suppose particle is projected from height y, it strikes the ground at a horizontal distance x, then distance
$R = \sqrt{x^{2} + y^{2}}$ ……..i

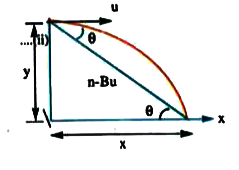
It t is the time of motion then
$x = u t$
and $y = \frac{1}{2} {gt}^{2}$
From equation (i) we get $t = \frac{x}{u}$
$∴ y = \frac{1}{2} t {g (\frac{x}{u})}^{2} = \frac{g x^{2}}{2 u^{2}}$ ........iii
From figure $\frac{y}{x} = tan θ$ or $y = x tan θ$ ........iv
From equation iii and iv we have
$x tan θ = \frac{g x^{2}}{2 u^{2}}$ or $x [\frac{g x}{2 u^{2}} - tan θ] = 0$
As x=0 is not possible
So $[\frac{g x}{2 u^{2}} - tan θ] = 0$ or $x = \frac{2 u^{2} tan θ}{g}$ ...........v
Now from equation i, iv and v we get
$R = \sqrt{x^{2} + y^{2}} = \sqrt{x^{2} + {(x tan θ)}^{2}} = x \sqrt{1 + {tan}^{2} θ} = x sec θ$ or $= \frac{2 u^{2}}{g} tan θ sec θ$

Updated on:21/07/2023

A ball is projected horizontally with a speed v from the top of the plane inclined at an angle $45^{\circ}$ with the horizontal. How far from the point of projection will the ball strikes the plane?
A $\frac{2 v^{2}}{g}$
B $\sqrt{2} [\frac{2 v^{2}}{g}]$
C $\frac{v^{2}}{g}$
D $\sqrt{2} \frac{v^{2}}{g}$
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

How far from the point of projection will the particle strike the plane?
A75m
B $\frac{65}{16} m$
C $\frac{75}{16} m$
D $\frac{85}{9} m$
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

What is the velocity of the particle just before it hits the plane?
A $5 \sqrt{3} m / s$
B $\frac{5}{2} \sqrt{13} m / s$
C $10 \sqrt{13} m / s$
D $5 \sqrt{26} m / s$