A rod AB of mass M is attached as shown in figure to a spring of constant k. A small block of mass mis placed on the rod at its free end A. In equilibrium, rod is horizontal, i.e., spring is stretched.
(a) If end A is moved down through a small distance d and released, determine the period of vibration,
(b) Determine the largest allowable value of d if the block m is to remain at all times in contact with the rod.
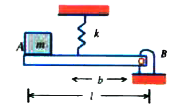
The correct Answer is:(a)T=2π ⎷l2(M3+m)kb2(b)g(M3+m)l2kb2
Let θ be the angular displacement of the rod when block is pushed by a small displacement x.
If x0 is the extension of the spring here , x0=lθandx=)=bθ
Restoring force in the spring = kx0
Restoring torque τ=(Kx0)b=Kb2θ
But τ=Iα where I=(Ml23+mL2)(M3+m)l2α=−kb2θ
α=−⎧⎨⎩Kb2M3+ml2⎫⎬⎭θ=2π√αθ
Topper's Solved these Questions
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
33 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PRACTICE EXERCISE - SPRINGS
16 Videos
Similar Questions
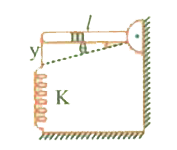
The end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View Solution
Knowledge Check
A uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 A12π√2kMB12π√kMC12π√6kMD12π√24kM
A12π√2kMB12π√kMC12π√6kMD12π√24kM
A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
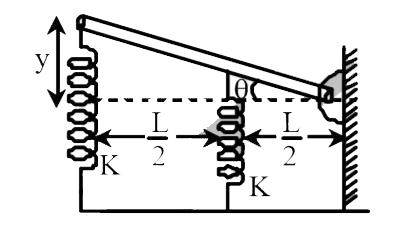
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

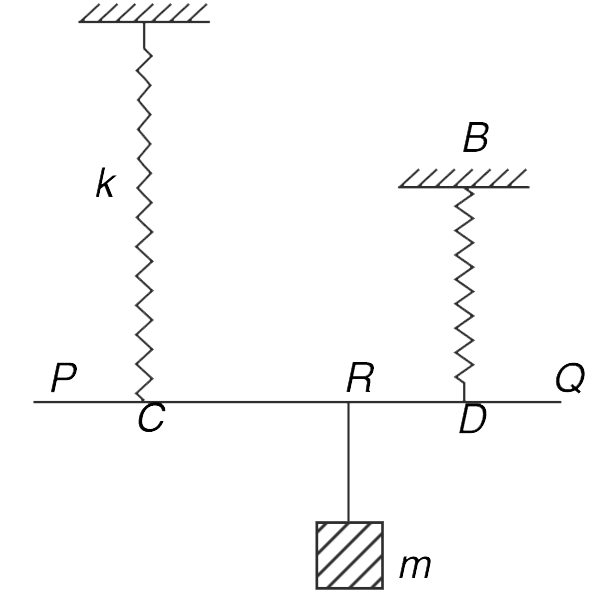
View SolutionTwo ideal springs of same make (the springs differ in their lengths only) have been suspended from points A and B such that their free ends C and D are at same horizontal level. A massless rod PQ is attached to the ends of the springs. A block of mass m is attached to the rod at point R. The rod remains horizontal in equilibrium. Now the block is pulled down and released. It performs vertical oscillations with time period T=2π√m3k where k is the force constant of the longer spring.
(a) Find the ratio of length RC and RD.
(b) Find the difference in heights of point A and B if it is given that natural length of spring BD is L.
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View Solution
