On the arrangement shown in figure Pulleys are small light and springs are ideal K1,K2,K3andK4 are force constant of the springs calculate period of small vertical oscillations of block of mass 'm'
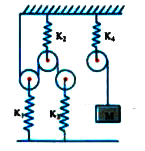
The correct Answer is:T=4π√m([1K1+1K2+1K3+1K4])
If the block is pulled down by a small displacement x and released , extra tension provides restoring force
Let T be the extra tension
Then T = ma
If x1,x2,x3andx4 are the extensions of springs.
2T=K1x1=K2x2=K3x3=K4x4
x=2(x1+x2+x3+x4)
x=4T(1K1+1K2+1K3+1K4)
from T = ma
4m(1K1+1K2+1K3+1K4)a=x,ω=√axandT=2πω
Topper's Solved these Questions
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
33 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PRACTICE EXERCISE - SPRINGS
16 Videos
Similar Questions
In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
View Solution
Knowledge Check
In the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
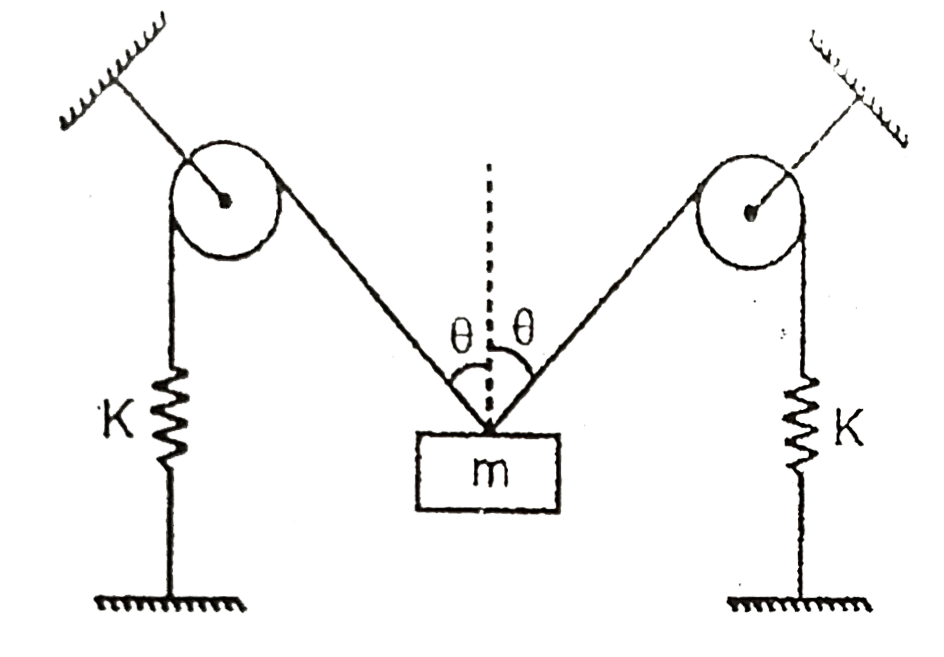A2πcosθ√m2kB2πsecθ√m2kC2πsinθ√m2kD2πcosecθ√m2k
In the arrangement shown if Fig. Pulleys are small and lught and spring are ideal and K1=25(π2)Nm, K2=2K1,K3= and K4=4K1 are the force constant of the spring. Calculate the period of small vertical oscillation of block of mass m=3kg.
View Solution-
In the arrangement shown if Fig. Pulleys are small and light and spring are ideal and K1=25(π2)Nm, K2=2K1,K3= and K4=4K1 are the force constant of the spring. Calculate the period of small vertical oscillation of block of mass m=3kg.
View Solution In the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
View SolutionThere is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2
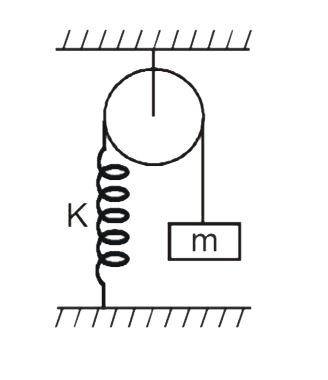
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
View Solution