An ideal monoatomic gas undergoes a process where its pressure is inversely proportional to its temperature (a) Calculate the specific heat for the process (b) Find the work done by two moles of gas if the temperature changes from $T_{1}$ to $T_{2}$

Text Solution

Verified by Experts

$\frac{7 R}{2}, 2 R (T_{2} - T_{1})$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - Problem
60videos
THERMODYNAMICS
BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 1A
135videos
THERMODYNAMICS
BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - NUMERICAL EXERCISE (LEVEL-2)
35videos
THERMODYNAMICS
BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2videos
THERMAL PROPERTIES OF MATTER
BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11videos
THERMOMETRY

Similar Questions

Knowledge Check

Question 1 - Select One
In a process the pressure of a gas is inversely proportional to the square of the volume. If temperature of the gas increases, then work done by the gas:
Ais positive
Bis negative
Cis zero
Dmay be positive
Question 2 - Select One
In a process, the pressure of an ideal gas is proportional to square of the volume of the gas. If the temperature of the gas increases in this process, then work done by this gas
A(a) is positive
B(b) is negative
C(c) is zero
D(d) may be positive or negative
Question 3 - Select One
One mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.

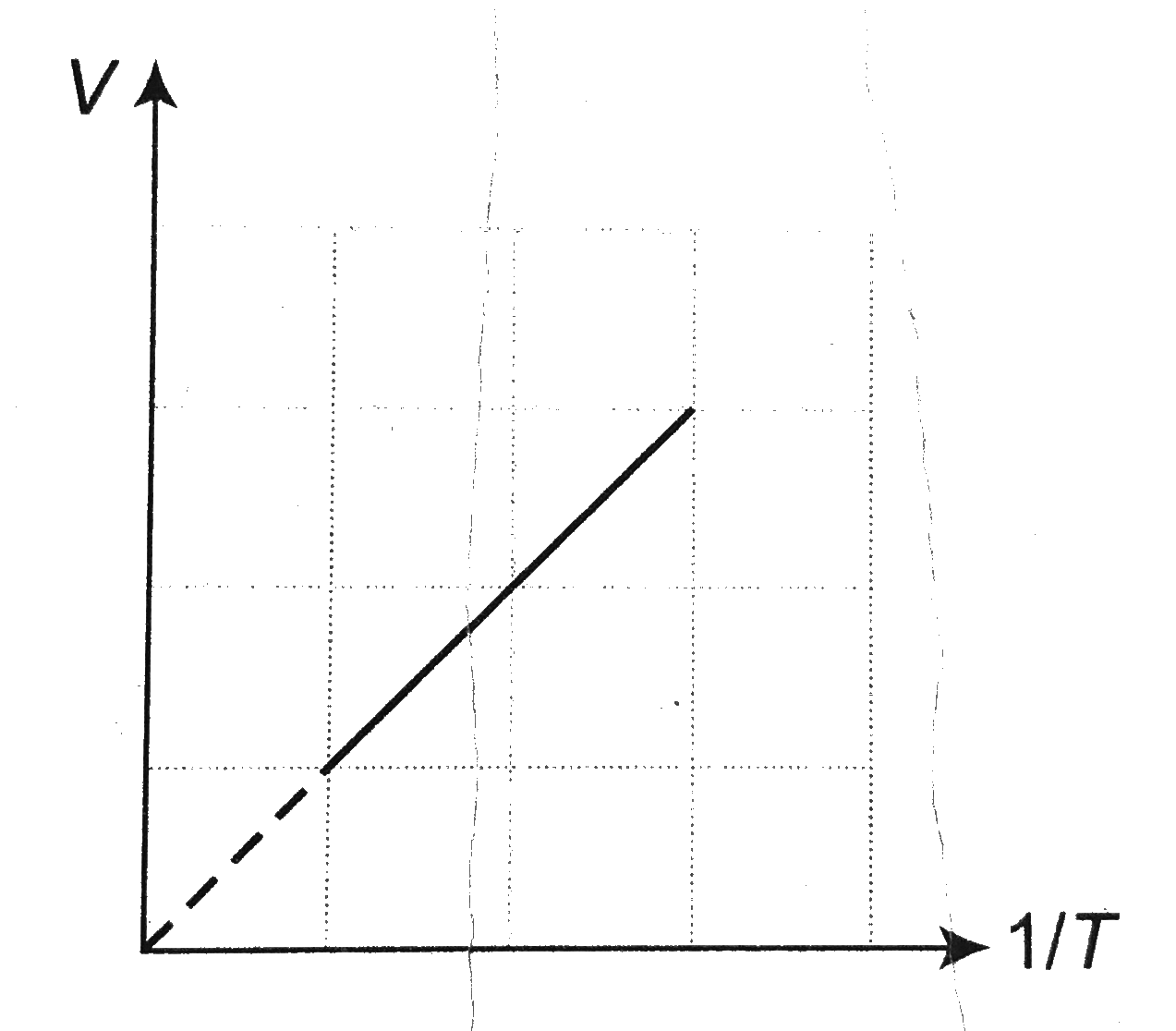
R is a gas constant.
A $\frac{3 R}{4}$
B $\frac{R}{2}$
C $\frac{R}{3}$
D $\frac{2 R}{3}$

AAKASH SERIES-THERMODYNAMICS-QUESTIONS FOR DESCRIPTIVE ANSWERS

Home
Ask Doubt
Profile