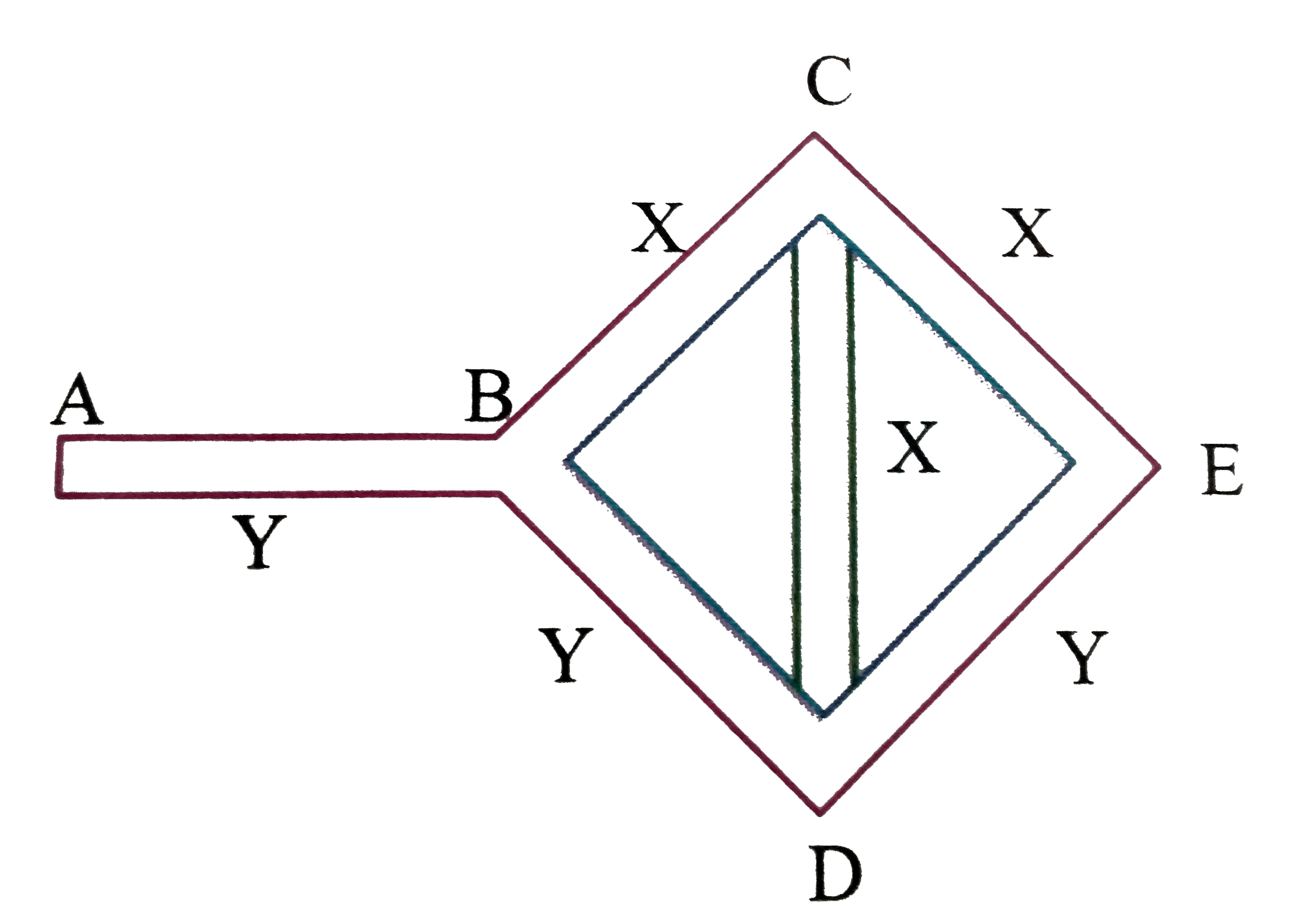
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1^(@)C^(-1)andtˆofyis400Wm^(-1)^(∘)C−1 .

It is clear from the symmerty of the figure that the points C and D are equivalent in all respect and hence, they are at the same temperature, say (theta). No heat will flow through the rod CD. We can, therefore, neglect this rod in further analysis.
Let l and A be the length and the area of cross section of each rod. The thermal resistances of AB, BC and BD are equal. Each has a value
R1=1KxlA . Similarly, thermal resistances of CE and DE are equal, each having a value
R2=1KylA . As the rod CD has no effect, we can say that the rods BC and CE are joined in sseries. Their equivalent thermal resistance is
R3=RBC+(RCE=R1+R2 . Also, the rods BD and DE together have an equivalent thermal resistance R4=RBD+(RDE=R1+R2 . The resistance R3 and R4 are joined in paralley and hence their equivalent thermal resistance is given by
1R5=1R3+1R4=1R3 . or, =R5=R32=R1+R22 . This resistance R5 is connected in series with AB. Thus, the total arrangement is equivalent to a thermal resistance
R=RAB+R5=R1+R1+R22=3R1+R22 . Figure shows the successive steps in this reduction.
. The heat current through A is
i=θA−θER=2(θA−θE)3R1+R2 . This current passes through the rod AB. We have
i=θA−θBRAB .or, θA−θB=(RAB)i . =R12(θA−θE)3R1+R2 . Putting from (i) and (ii), θA−θB=2Ky(θA−θE)Kx+R2 . =2×400800+3×400×50∘C=20∘C . or, θB=θA−20∘C=40∘C .

Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Short Answer
11 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Objective 1
10 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View Solution
Knowledge Check
Three rods of material 'x' and three rods of materialy are connected as shown in All the rods are of identical length and cross section If the end A is maintained at 60∘C and the junction E at 10∘0C find effective Thermal Resistance Given length of each rod =1 area of cross-section =A conductivity of x=K and conductivity of y=2K
 .A4l3KAB7l6KAC4KA3lD7KA3l
.A4l3KAB7l6KAC4KA3lD7KA3lSeven identical rods of material of thermal conductivity K are connected as shown in figure. All the rods are of identical length L and cross sectional area A1. If one end A is kept at 100∘C and the other end B is kept at 0∘C, what would be the temperature of the junctions C, D and E (TC,TD and TE) in the steady state?
 ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
Seven identical rods of material of thermal conductivity k are connected as shown in Fig. All the rods are of identical length l and cross sectional area A If the one end B is kept at 100∘C and the other end is kept at 0∘C what would be the temperatures of the junctions C, D and E(θC,θ)D and θE) in the steady state?AθC>θE>θDBθE=50∘C and θD=37.5∘CCθE=50∘C,θC=62.5∘C and θD=37.5∘CDθE=50∘C,θC=60∘C and θD=40∘C
Two rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

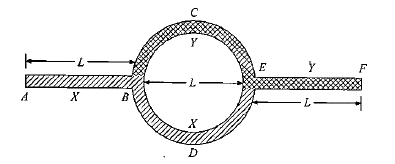
View SolutionFew rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1^(@)C^(-1)andtˆofsteel=46Wm^(-1)(∘)C−1 .

View SolutionSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .
.
View SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

View Solution
