A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l/4 . The pendulum is released from rest. Throughout the motion the moving string makes small angle with vertical. Find the time after which the pendulum returns back to its initial position.
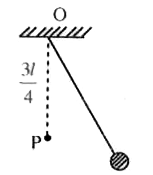
After P length of pendulum becomes 14 Now as T∝√l , So after P time period will become T1=T/2. Therefore, the desired time will be :
t=T2+T2=T2+T4=3T4
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II
175 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
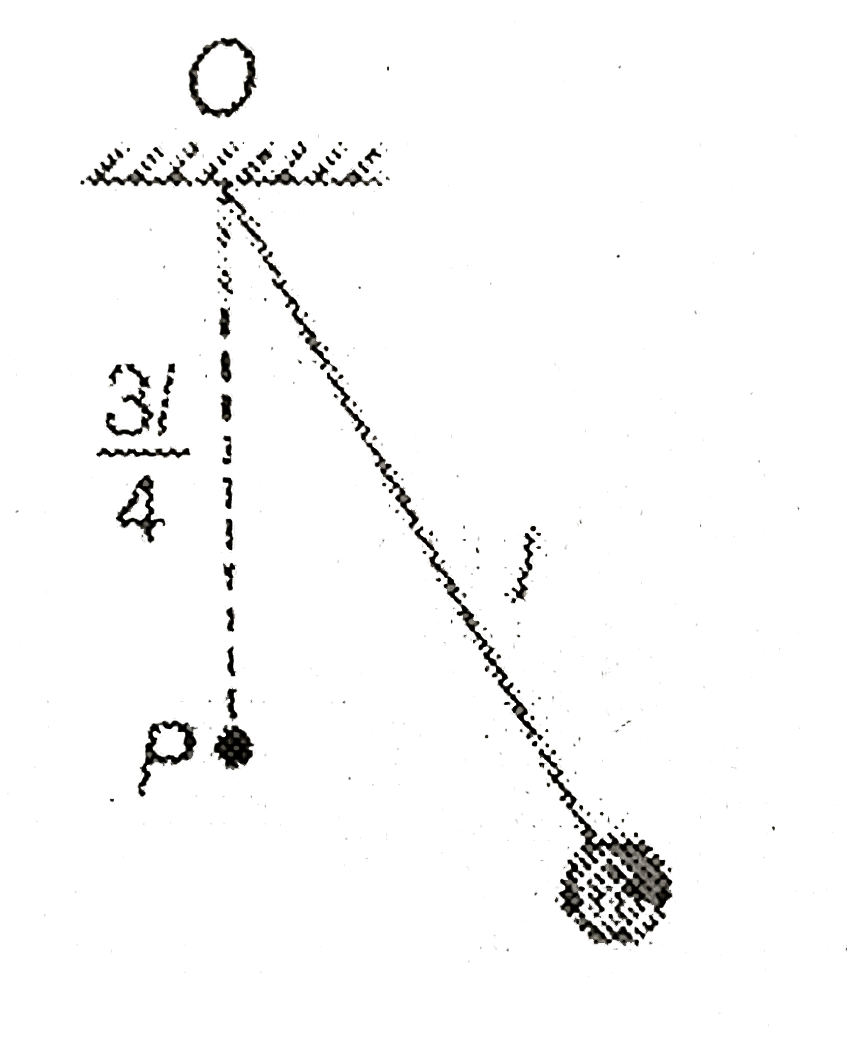
View SolutionA simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
View Solution
Knowledge Check
A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
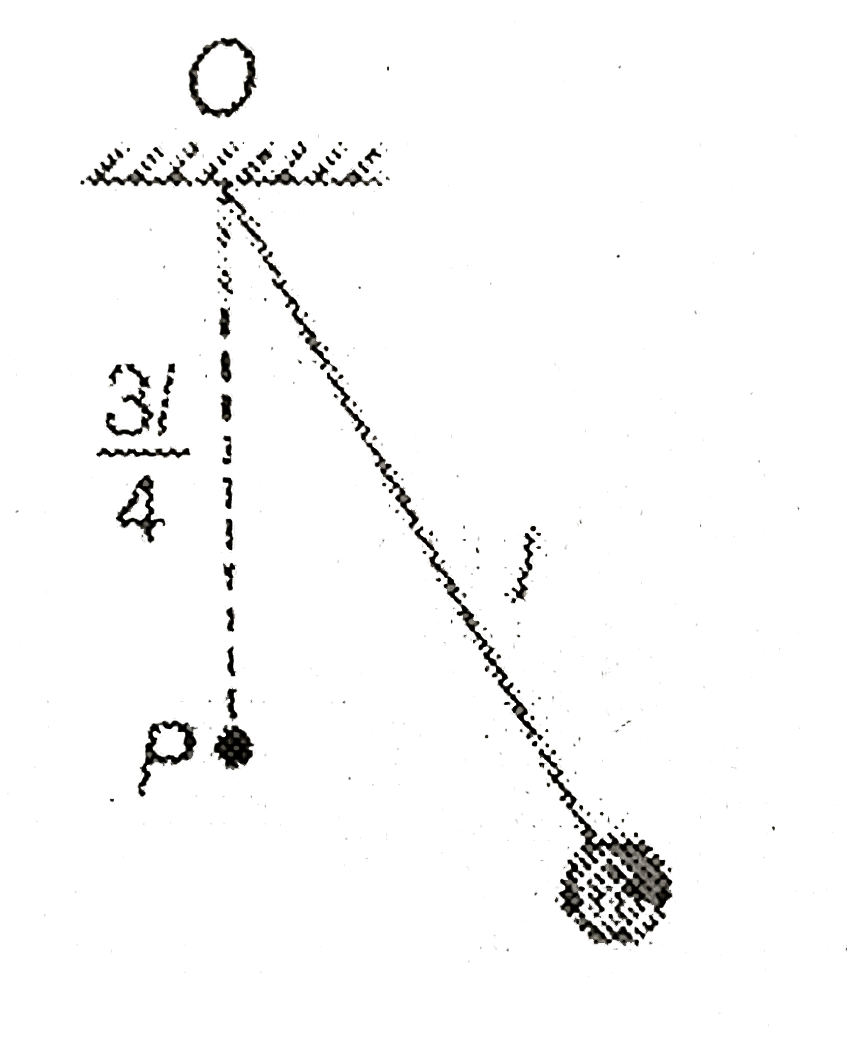 ATB3T4C3T5D4T5
ATB3T4C3T5D4T5A simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle θ with the vertical, the angle θ which the acceleration vector of the bob makes with the string is given by–
 Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2
Aϕ=0Bφ=tan−1(tanθ2)Cφ=tan−1(2tanθ)Dφ=π/2A simple pendulum has time period T. Charges are now fixed at the point of suspension of the pendulum and on the bob. If the pendulum continues to oscillate, its time period will now be
Agreater than TBequal to TCless than TDeither (a) or (c) depending on whether the charges attract or repel each other
A simple pendulum of length l and mass m free to oscillate in vertical plane. A nail is located at a distance d=l−a vertically below the point of suspension of a simple pendulum. The pendulum bob is released from the position where the string makes an angle of 90∘ from vertical. Discuss the motion of the bob if (a) l=2a and (b) l=2.5a.
View SolutionA nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of 60∘ with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.
View SolutionA pendulum has a period T for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

View SolutionA pendulum has a period T for small osillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

View SolutionA heavy small sized sphere is suspended by a string of length l . The sphere rotates uniformly in a horizontal circle with the string making an angle θ with the vertical. Then the time period of this conical pendulum is-
View Solution
