A block is placed on a horizontal platform. The system is making horizontal oscillations about a fixed point with a frequency of 0.5Hz. The maximum amplitude of oscillation if the block is not to slide on the horizontal platform, is (Coefficient of friction between the block and the platform = 0.4)
0.3971m
0.4871m
0.2971m
0.5271m
The correct Answer is:A
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE -II Simple pendulum
23 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE -II SPRINGS
19 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE -I ASSERTION & REASON TYPE QUESTIONS
19 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
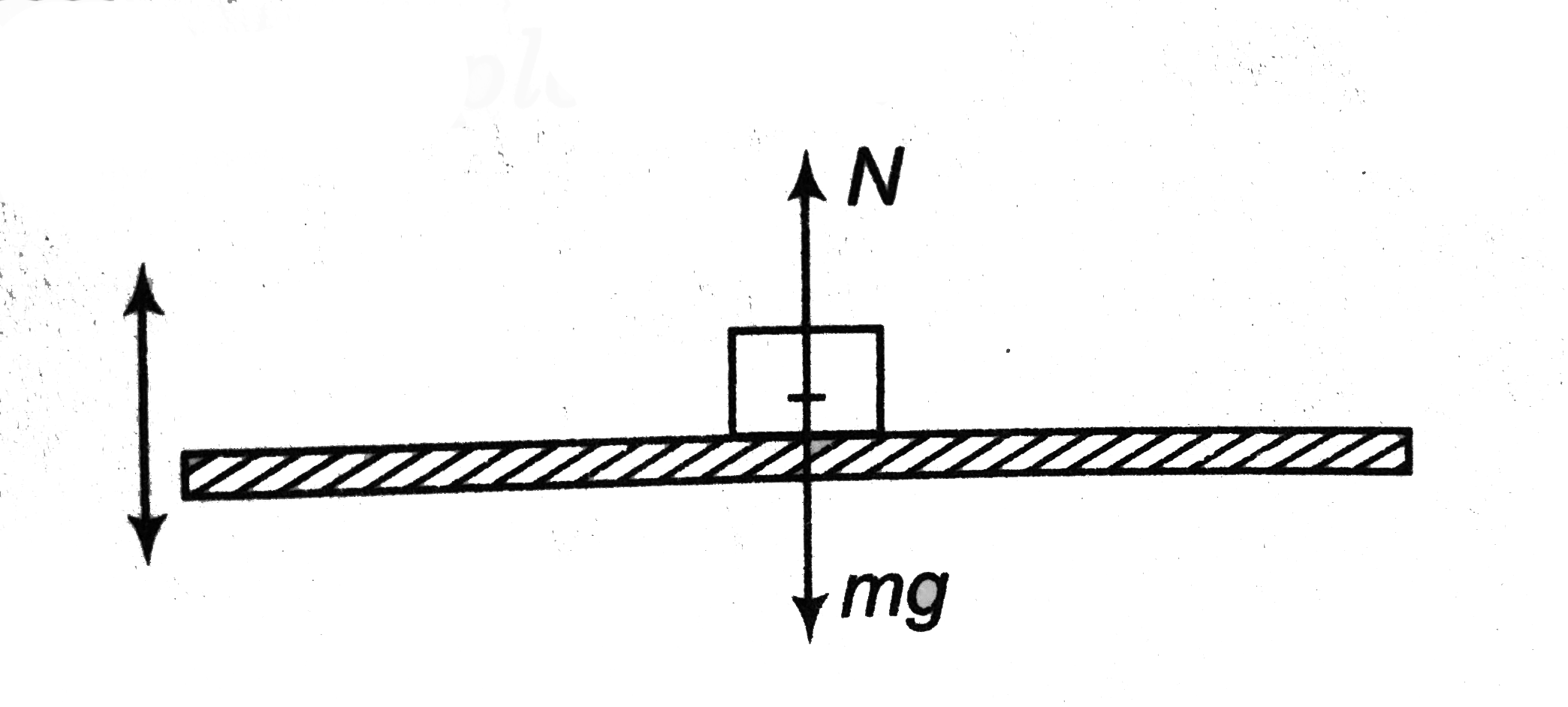
View SolutionA block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.

View Solution
Knowledge Check
A block of 0.5kg is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of 0.5Hz. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly
A0.5mB0.75mC1mD1.2mA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
A(a) at the mean position of the platformB(b) for an amplitude of gω2C(c) for an amplitude of g2ω2D(d) at the highest position of the platformA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
Aat the highest position of the platformBat the mean position of the platformCfor an amplitude of gω2Dfor an amplitude of g2ω2
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionA block is placed on a platform which is making oscillations with amplitude of 10cm along a vertical line.The least period of oscillation of platform so that it will not get separated from the platform is
View SolutionA horizontal platform is undergoing vertical S.H>M of time period T. A block of mass M is placed on the platform . The maximum mplitude of the platform so that the block is not detached form it is
View Solution
