A long, thin bar (α,L0) is clamped rigidly at its ends at temperature θ0. When the temperature (θ) is increased, the expanding bar will bow out as shown. If the bowing is not too large, a fair first approximation to the shape of the bar is two equal straight segments in the form of a wide V. The arc of the bow (elevation) y0 as a function of θ is expressed as y0=L02√Kα(θ−θ0) where K=______
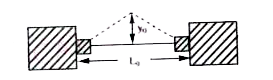
The correct Answer is:2
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF LIQUIDS (LECTURE SHEET) Straight Objective Type Questions15videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF LIQUIDS (LECTURE SHEET) More than One correct answer Type Questions2videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Matrix Matching Type Questions)2videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 333videos
THERMODYNAMICS
Similar Questions
A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionA metal bar of length L and area of cross-section A is rigidly champed between two walls. The Young's modulus of its material is Y and the coefficient of linear expansion is α. The bar is heated so that its temperature is increased by θ∘C. Find the force exerted at the ends of the bar.
View Solution
Knowledge Check
- Question 1 - Select One
2.¯6−0.¯¯¯¯82 is equal to
A181999B18299C8299DNone of these - Question 2 - Select One
The ends of a thin bar are maintained at different temperatures. The temperature of the cooler end is 11∘C , while the temperature at a point 0.13m from the cooler end is 23∘C and the temperature of the warmer end is 48∘C. Assuming that heat flows only along the length of the bar ( the sides are insulated), find the length of the bar.
A0.50mB0.40mC0.23mD0.64m - Question 3 - Select One
A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22))
An arrow shots from a bow with velocity v at an angle θ with the horizontal range R . Its range when it is projected at angle 2θ with the same velocity is
View SolutionThe ends of a long bar are maintained at different temperatures and there is no loss of heat from the sides of the bar due to conduction or radiation. The graph of temperature against distance of the bar when it has attained steady state is shown here. The graph shows (i) the temperature gradient is not uniform.
(ii) the bar has uniform cross-sectional area.
(iii) the cross-sectional area of the bar increases as the distance from the hot end increases.
(iv) the cross-sectional area of the bar becreases as the distance from the hot end increasesView SolutionAssume that the coefficient of linear expansion of the material of a rod remains constant, equal to α∘C−1 for a fairly large range of temperature. Length of the rod is L0 at temperature θ0. (a) Find the length of the rod at a high temperature θ. (b) Approximate the answer obtained in (a) to show that the length of the rod for small changes in temperature is given by L=L0[1+α(δ−δ0)]
View SolutionA man holds a thin sticks at its two ends and bends it in an arc, like a bow without a string. Which of the following figures correctly show the directions of the forces exerted by him on the stick? ( Neglect gravity)
View SolutionAn arrow shots from a bow with velocity v at an angle θ with the horizontal range R . Its range when it is projected at angle 2θ with the same velocity is
View Solution

