The ends of a long bar are maintained at different temperatures and there is no loss of heat from the sides of the bar due to conduction or radiation. The graph of temperature against distance of the bar when it has attained steady state is shown here. The graph shows (i) the temperature gradient is not uniform.
(ii) the bar has uniform cross-sectional area.
(iii) the cross-sectional area of the bar increases as the distance from the hot end increases.
(iv) the cross-sectional area of the bar becreases as the distance from the hot end increases
i & ii
ii & iii
i & iv
ii & iv
The correct Answer is:C
To solve the problem, we need to analyze the given information about the long bar that is maintained at different temperatures at its ends and understand the implications of the temperature gradient and the cross-sectional area.
1. Understanding the Steady State Condition:
- In steady state, the temperature distribution along the bar does not change with time. The heat transfer through the bar reaches a constant value.
- Since there is no heat loss from the sides, the heat current (rate of heat transfer) remains constant throughout the bar.
2. Analyzing the Temperature Gradient:
- The graph shows temperature (T) plotted against distance (x) from the hot end of the bar.
- If the graph is not a straight line (for example, it is parabolic), it indicates that the temperature gradient (dT/dx) is not uniform. This means that the rate of temperature change with respect to distance varies along the length of the bar.
3. Using Fourier's Law of Heat Conduction:
- According to Fourier's law, the heat current (dq/dt) can be expressed as:
dqdt=kAdTdx
- Here, k is the thermal conductivity, A is the cross-sectional area, and dT/dx is the temperature gradient.
- Since dq/dt is constant, if dT/dx changes, then A must also change to keep the product A⋅dTdx constant.
4. Determining the Cross-Sectional Area:
- If the temperature gradient (dT/dx) increases as we move from the hot end to the cold end, then the cross-sectional area A must decrease to maintain a constant heat current.
- This leads us to conclude that the cross-sectional area of the bar decreases as the distance from the hot end increases.
5. Evaluating the Statements:
- (i) The temperature gradient is not uniform: True (as indicated by the graph).
- (ii) The bar has a uniform cross-sectional area: False (as we concluded that the area decreases).
- (iii) The cross-sectional area of the bar increases as the distance from the hot end increases: False.
- (iv) The cross-sectional area of the bar decreases as the distance from the hot end increases: True.
6. Final Conclusion:
- The true statements are (i) and (iv). Therefore, the correct answer is that statements 1 and 4 are true.
- In steady state, the temperature distribution along the bar does not change with time. The heat transfer through the bar reaches a constant value.
- Since there is no heat loss from the sides, the heat current (rate of heat transfer) remains constant throughout the bar.
- The graph shows temperature (T) plotted against distance (x) from the hot end of the bar.
- If the graph is not a straight line (for example, it is parabolic), it indicates that the temperature gradient (dT/dx) is not uniform. This means that the rate of temperature change with respect to distance varies along the length of the bar.
- According to Fourier's law, the heat current (dq/dt) can be expressed as:
dqdt=kAdTdx
- Here, k is the thermal conductivity, A is the cross-sectional area, and dT/dx is the temperature gradient.
- Since dq/dt is constant, if dT/dx changes, then A must also change to keep the product A⋅dTdx constant.
- If the temperature gradient (dT/dx) increases as we move from the hot end to the cold end, then the cross-sectional area A must decrease to maintain a constant heat current.
- This leads us to conclude that the cross-sectional area of the bar decreases as the distance from the hot end increases.
- (i) The temperature gradient is not uniform: True (as indicated by the graph).
- (ii) The bar has a uniform cross-sectional area: False (as we concluded that the area decreases).
- (iii) The cross-sectional area of the bar increases as the distance from the hot end increases: False.
- (iv) The cross-sectional area of the bar decreases as the distance from the hot end increases: True.
- The true statements are (i) and (iv). Therefore, the correct answer is that statements 1 and 4 are true.
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Thermal Physics) (Kinetic theory of gasess)
Explore 12 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Thermal Physics) (Thermodynamic process)
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Thermal Physics) (Calorimetry)
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
View SolutionA uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
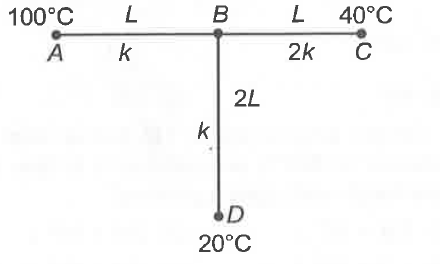
View SolutionFind the temperature of junction at B, if each rod has equal area of cross-section.
View SolutionA cylindrical conductor of length l and uniform area of cross-section A has resistance R. Another conductor of length 2l and resistance R of the same material has area of cross-section :
View SolutionA steel bar of cross-sectional area A and length l is magnetised to develop an intensity of magnetisation l . The pole strength of the bar is
View SolutionA rod is made of uniform material and has non-uniform cross section. It is fixed at both the ends as shown and heated at mid-section. Which of the following are not correct?

View SolutionConsidering a wire of non-uniform cross-section as shown.If the area of cross-section at A is double of the area of cross-section at point B.Ratio of heat energy dissipated in a unit volume per unit time at points A and B is
_PHY_E05_279_Q01.png)
View SolutionBars of two different metals are bolted together , as shown in figure. The distance x does not change with temperature if :-
_E01_015_Q01.png)
View SolutionAn irregular rod of same uniform material as shown in figure is conducting heat at a steady rate. The temperature gradient at various sections versus area of cross section graph will be
_S01_094_Q01.png)
View SolutionA uniform bar of square cross-section is lying along a frictionless horizontal surface. A horizontal force is applied to pull it from one of its ends then

View Solution
