तीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
कथन-1 सत्य है, कथन-2 सत्य है, कथन-2 कथन-1 का सही स्पष्टीकरण है।
कथन-1 सत्य है, कथन-2 सत्य है, कथन-2, कथन-1 का सही स्पष्टीकरण नहीं है।
कथन-1 सत्य है, कथन-2 असत्य है
कथन-1 असत्य है कथन-2 सत्य है
The correct Answer is:D
Step by step video, text & image solution for तीन समतल लीजिए P_(1) : x-y +z=1 P_(2): x+y -z=-1 P_(3): x-3y + 3z=2 माना L_(1), L_(2), L_(3) क्रमशः समतल P_(2) व P_3, P_3 व P_(1) तथा P_(1) व P_(2) की प्रतिच्छेदी रेखायें हैं। कथन-1: L_(1), L_(2) और L_(3) में से कम से कम दो रेखायें असमान्तर हैं। क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है। by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
यदि रेखा x−1−3=y−22k=z−32 तथा x−13k=y−51=z−6−5 परस्पर लम्बवत् हो, तो k=
View Solutionयदि सिक्का 'n' बार उछाला जाता है , तो चित आने की प्रायिकता 'p' है। माना pn दो या अधिक बार लगातार चित नहीं आने की प्रायिकता है। सिद्ध कीजिए कि p1=1,p2=1−p2 तथा pn=(1−p)pn−1+p(1−p)pn−2 यदि n≥3 है।
View SolutionConsider the lines L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 and the planes P1=7x+y+2z=3,P2:3x+5y−6z=4. Let ax+by+cz=d be the equation of the plane passing through the point of intersection of lines L1andL2, and perpendicular to planes P1andP2.
Match Column I with Column II.

View SolutionP1andP2 are planes passing through origin, L1andL2 are two lines on P1andP2 respectivelym such that their intersection is the origin. Show that there exist points, A, B and C , whose perpmutation, A, B' and C' respectively, can be chosen such that (i) A is on L1'BandP1 put not on L1andC not on P1 , (ii) A is on L2,B'onP2 but not on L2andC' not on P2 .
View SolutionP1andP2 are planes passing through origin, L1andL2 are two lines on P1andP2 respectivelym such that their intersection is the origin. Show that there exist points, A, B and C , whose perpmutation, A, B' and C' respectively, can be chosen such that (i) A is on L1'BandP1 put not on L1andC not on P1 , (ii) A is on L2,B'onP2 but not on L2andC' not on P2 .
View SolutionConsider three planes P1:x−y+z=1
P2:x+y−z=−1
and P3:x−3y+3z=2
Let L1,L2,L3 be the lines of intersection of the planes P2 and P3,P3 and P1,P1 and P2 respectively.
Statement I Atleast two of the lines L1,L2 and L3 are non-parallel.
Statement II The three planes do not have a common point.
View SolutionConsider two intersecting (non-perpendicular lines L1=0andL2=0 and a point P1. Image of P1 and L1=0 is P2, image of P2 in L2=0 is P3 , image of P3 in L1 =0 is P4 and so on. Which of the following statements are incorrect ?
View SolutionLet P1andP2 be two planes containing the lines L2andL2 respectively.
STATEMENT-1 : If P1andP2 are parallel then L1andL2 must be parallel.
and
STATEMENT-2 : If P1andP2 are parallel the L1andL2 may not have a common point.
View Solutionतीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
View SolutionNumber of units of three different products P1,P2andP3 produced (nits in hundreds) at four different locations (L1,L2=L3andL4)
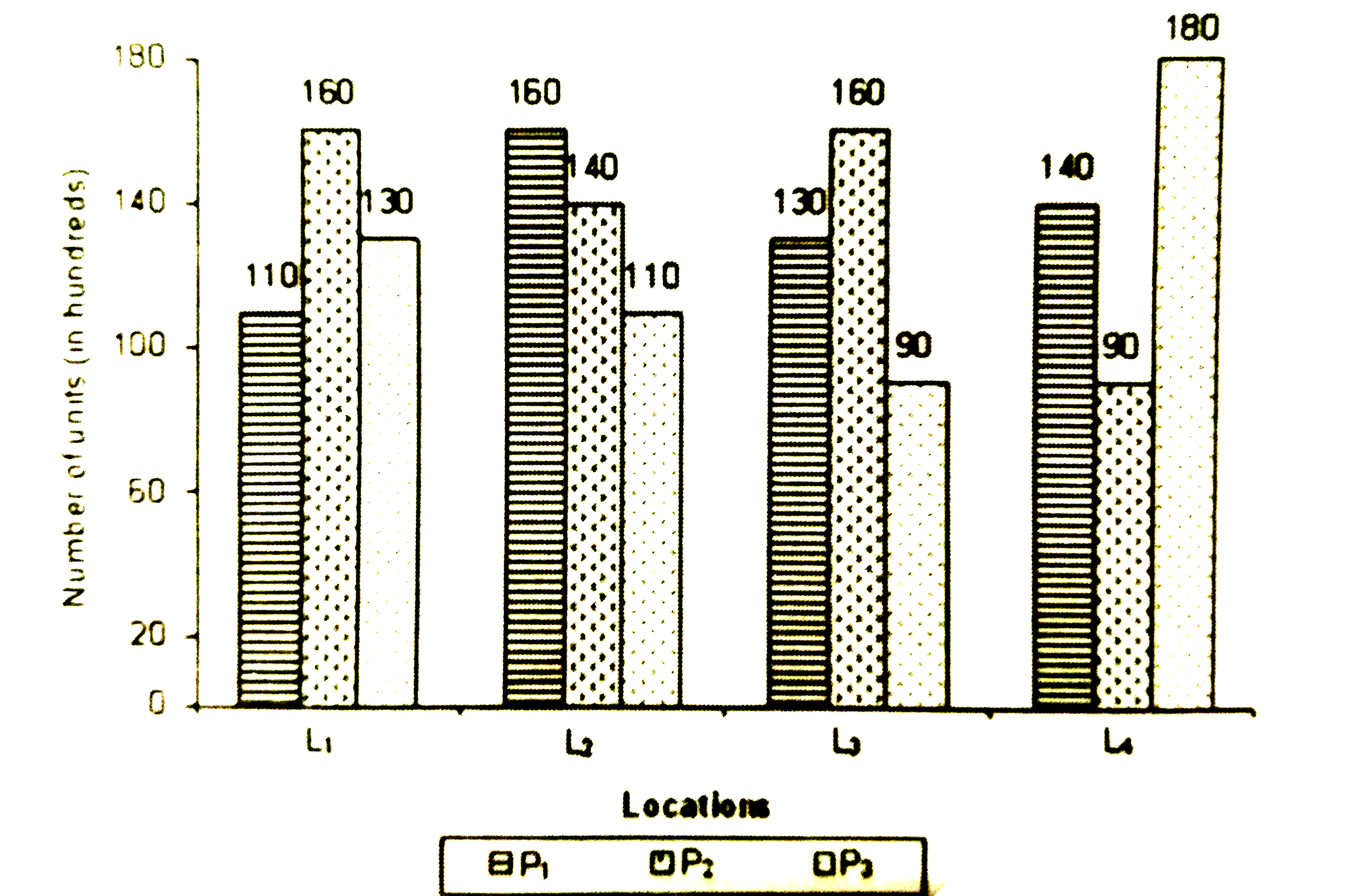
What is the average number of units (in hundreds of P1 produced per location ?
View Solutionरेखायें l1 व l2 प्रतिच्छेदी है तो उनके बीच की न्यूनतम दूरी होगी -
View Solutionतीन समतल
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2 पर विचार कीजिए।
L1,L2 व L3 क्रमशः समतलों P2 व P3,P3 व P1 एवं P1 व P2 की प्रतिच्छेदन रेखाएं है।
कथन1: रेखाओं L1,L2 व L3 में से कम से कम दो रेखाएं असमांतर है।
कथन 2:तीनों समतलों का कोई भी उभयनिष्ठ बिंदु नहीं है।
View SolutionConsider the lines L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 and the planes P1=7x+y+2z=3,P2:3x+5y−6z=4. Let ax+by+cz=d be the equation of the plane passing through the point of intersection of lines L1andL2, and perpendicular to planes P1andP2.
Match Column I with Column II.

View Solutionतीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
View Solutionतीन समतल
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2 पर विचार कीजिए।
L1,L2 व L3 क्रमशः समतलों P2 व P3,P3 व P1 एवं P1 व P2 की प्रतिच्छेदन रेखाएं है।
कथन1: रेखाओं L1,L2 व L3 में से कम से कम दो रेखाएं असमांतर है।
कथन 2:तीनों समतलों का कोई भी उभयनिष्ठ बिंदु नहीं है।
View Solutionतीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
View Solution
