A small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
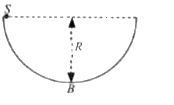
The fraction of translational kinetic energy at the sphere is 5/7.
The fraction of rotational kinetic energy of the sphere is 2/7.
The fraction of rotational kinetic energy of the sphere is 27mv2.
The total kinetic energy of the sphere at the bottom of the bowl is 27mv2
The correct Answer is:A, B, C
Let the linear and angular velocities of the small sphere S be v and co respectively when it reaches the bottom of the bowl B.
At this position (bottom of B), the translational kinetic energy of the sphere is given by
E1=12mv2, where m is the mass of the sphere.
As the sphere rolls down without slipping, we have, v=rω, r is the radius of the sphere.
∴E2=15mr2ω2=15mv2
Therefore, total kinetic energy of the sphere at the bottom of the bowl is
E=E1+E2=12mv2+15mv2=710mv2
Fraction of translational kinetic energy of the sphere
=E1E=12mv2710mv2=57
Fraction of rotational kinetic energy of the sphere
=E2E=15mv2710mv2=27
Topper's Solved these Questions
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions
17 Videos
- MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONBOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions
17 Videos
- MODEL TEST PAPTER BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPTER EXERCISE - MCQs
80 Videos
- NUCLEAR PHYSICBOOK - MTG-WBJEECHAPTER - NUCLEAR PHYSICEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
5 Videos
Similar Questions
A small sphere of mass m and radius r rolls without slipping on the insides of a large hemisphere of radius R whose axis of symmetry is vertical. Its starts at the top from rest. What is the kinetic energy of the small sphere at the bottom? What fraction is rotational and what transiational? What normal force does the small spheres exert on the hemisphere at the bottom?
[Hint: consider circular motion of center of mass at the bottom to calcualte normal reaction. For others consider conservation of energy.?
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View Solution
Knowledge Check
A small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
 .A107mgB177mgC57mgD75mg
.A107mgB177mgC57mgD75mgA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at BA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
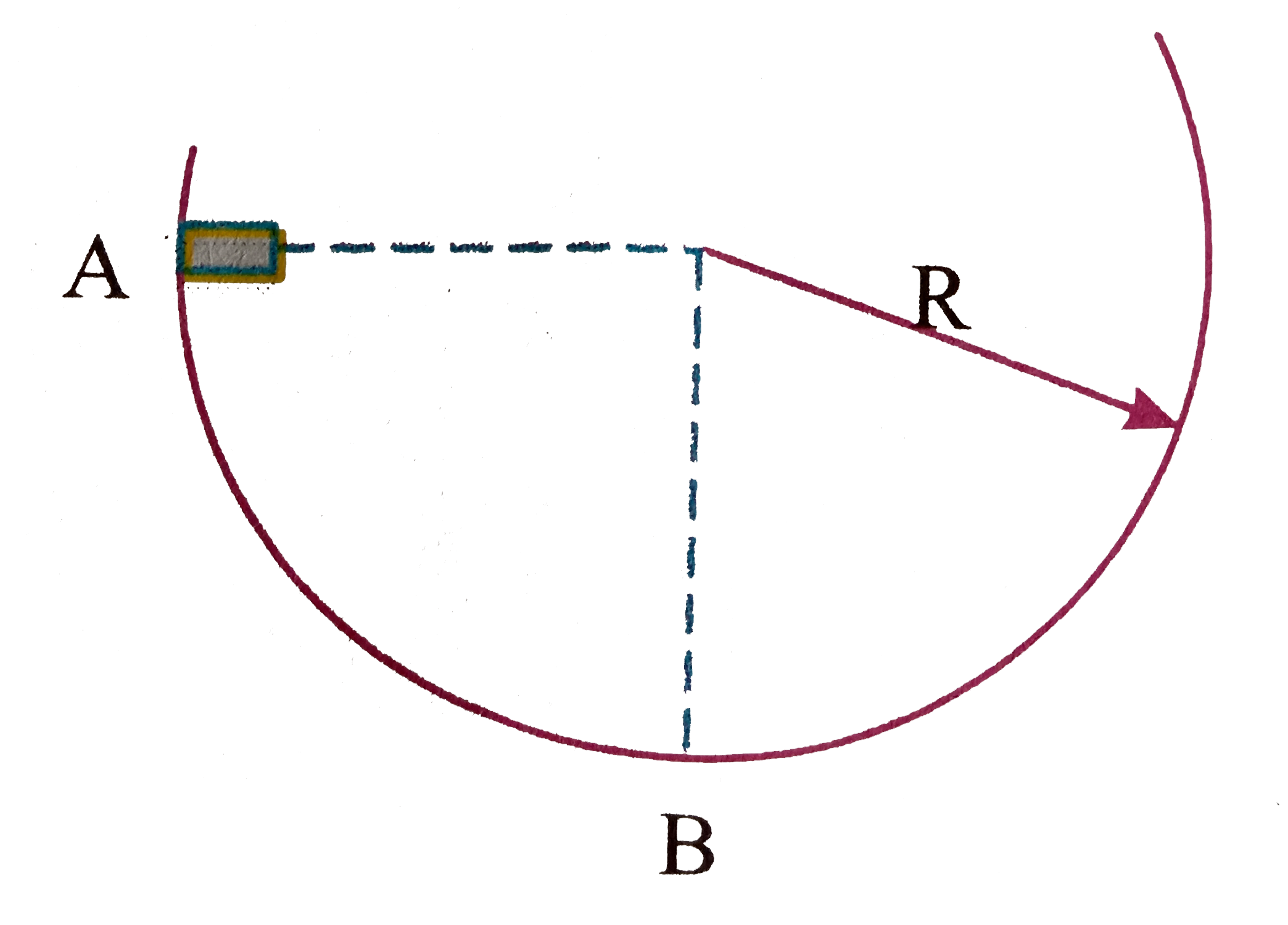 Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
A small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
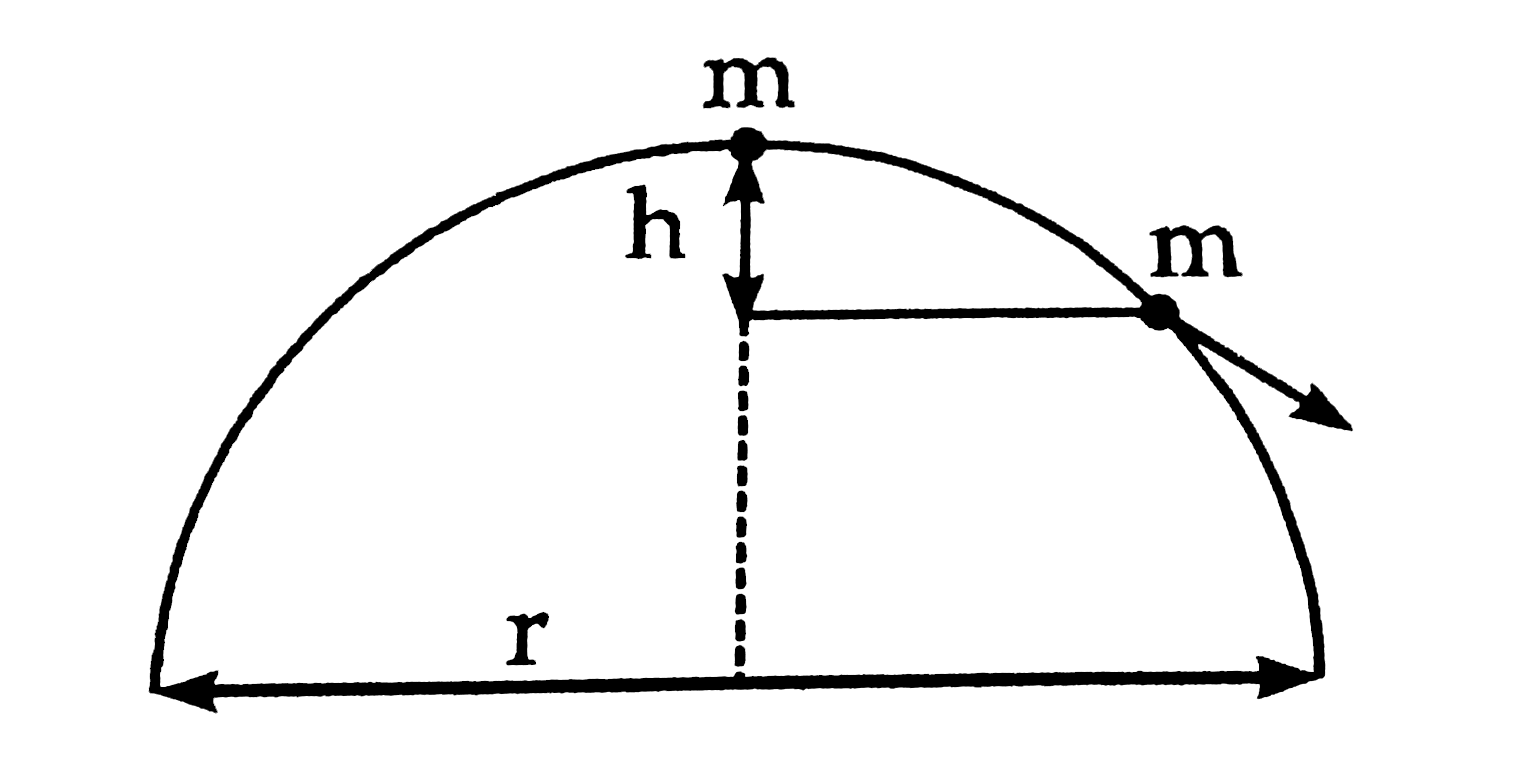
View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
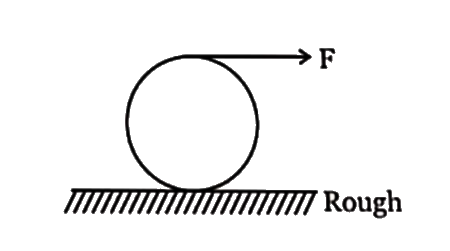
View SolutionA solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
View SolutionA small steel sphere of mass m and radius r rolls without slipping on the fiictionless surface of a large hemisphere of radius R{R gt gt r) whose axis of symmetry is vertical. It starts at the top from the rest, (a) What is the kinetic energy at the bottom ? (b) What fraction is the rotational kinetic energy of the total kinetic energy at the bottom? (b) What fraction is the rotational kinetic energy of the total kinetic energy? (c) What fraction is the translational kinetic energy of the total kinetic energy? (d) Calculate the normal force that the small sphere will exerton.the hemisphere at its bottom. Howthe results will be affected if r is not very sjnall as compared to R.
View SolutionA small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
View Solution
