A smooth massless string passes over a smooth fixed pulley. Two masses m1 and $m_{2} (m_{1} > m_{2})$ are tied at the two ends of the string. The masses are allowed to move under gravity starting from rest. The total external force acting on the two masses is

A

$(m_{1} + m_{2}) g$

B

$\frac{{(m_{1} - m_{2})}_{1}^{2}}{m_{1} + m_{2}} g$

C

$(m_{1} - m_{2}) g$

D

$\frac{{(m_{1} + m_{2})}_{1}^{2}}{m_{1} - m_{2}} g$

Text Solution

Verified by Experts

The correct Answer is:B

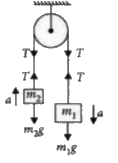
Let a be the common acceleration of the system and T be the tension in the string.
The equations of motion of two masses are
$m_{1} g - T = m_{1} a$ …(i)
$T - m_{2} g = m_{2} a$ …(ii)
Adding eqn. (i) and eqn. (ii), we get
$a = \frac{(m_{1} - m_{2})}{m_{1} + m_{2}} g$ ...(iii)
Acceleration of centre of mass of the system is
$a_{C M} = \frac{m_{1} a_{1} + m_{2} a_{2}}{m_{1} + m_{2}} = \frac{m_{1} a - m_{2} a}{m_{1} + m_{2}}$
( $∵ a_{1}$ and $a_{2}$ are equal in magnitude but opposite in direction)
$a_{C M} = (\frac{m_{1} - m_{2}}{m_{1} - m_{2}}) a = (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) (\frac{m_{1} - m_{2}}{m_{1} + m_{2}}) g$ (Using (iii))
$= {(\frac{m_{1} - m_{2}}{m_{1} + m_{2}})}^{2} g$
The total external force acting on the two masses is
$F_{ext} = (m_{1} + m_{2}) a_{C M} = (m_{1} + m_{2}) {(\frac{m_{1} + m_{2}}{m_{1} + m_{2}})}^{2} g$
$= \frac{{(m_{1} - m_{2})}_{1}^{2}}{m_{1} + m_{2}} g$

|

Updated on:21/07/2023

Class 12 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A light string passing over a smooth light pulley connects two blocks of masses $m_{1}$ and $m_{2}$ (vertically). If the acceleration of the system is $g / 8$ , then the ratio of masses is
A $8 : 1$
B $4 : 3$
C $5 : 3$
D $9 : 7$
Question 2 - Select One
Two masses $m_{1}$ and $m_{2}$ are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming $m_{1} > m_{2}$ acceleration of the system is:

A $\frac{m_{1} g {sin θ}_{1} + m_{2} g {sin θ}_{2}}{m_{1} + m_{2}}$
B $\frac{m_{1} g {sin θ}_{1} - m_{2} g {sin θ}_{2}}{m_{1} - m_{2}}$
C $\frac{m_{1} g {sin θ}_{1} - m_{2} g {sin θ}_{2}}{m_{1} + m_{2}}$
D $\frac{(m_{1} + m_{2}) ({sin θ}_{1} + {sin θ}_{2}) g}{m_{1} - m_{2}}$
Question 3 - Select One
A light string passing over a smooth light pulley connects two blocks of masses $m_{1}$ and $m_{2}$ (vertically). If the acceleration of the system is $g / 8$ , then the ratio of the masses is
A $8 : 1$
B $9 : 7$
C $4 : 3$
D $5 : 3$

MTG-WBJEE-MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTION-WB-JEE Previous years questions

Home
Ask Doubt
Profile