Three identical square plates rotate about the axes shown in the figure in such a way that their kinetic energies are equal. Each of the rotation axes passes through the centre of the square. Then the ratio of angular speeds $ω_{1} : ω_{2} : ω_{3}$ is

A

$1 : 1 : 1$

B

$\sqrt{2} : \sqrt{2} : 1$

C

$1 : \sqrt{2} : 1$

D

$1 : 2 : \sqrt{2}$

Text Solution

Verified by Experts

The correct Answer is:B

Kinetic energy of rotation, $K_{R} = \frac{1}{2} I ω^{2}$
or $ω^{2} = \frac{2 K_{R}}{I}$
Since $K_{R}$ remains the same for all three configurations,
$∴ ω \propto \frac{1}{\sqrt{l}}$
Let m be the mass and a be side of each square plate
In figure 1, moment of inertia about the given axis,

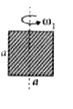
$I_{1} = \frac{1}{12} m a^{2}$
In figure 2, moment of inertia about
the given axis,
$I_{2} = \frac{1}{12} m a^{2}$

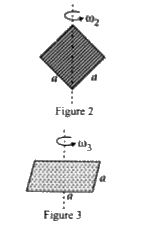
In figure 3, moment of inertia
about the given axis
$I_{3} = \frac{1}{6} m a^{2}$
$∴ I_{1} : I_{2} : I_{3} = 1 : 1 : 2$
As $ω \propto \frac{1}{\sqrt{l}}$
$∴ ω_{1} : ω_{2} : ω_{3} = 1 : 1 : \frac{1}{\sqrt{2}} = \sqrt{2} : \sqrt{2} : 1$

|

Updated on:21/07/2023

Class 12 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed $ω$ . Its rotational kinetic energy is
A $\frac{1}{2} M R^{2} ω^{2}$
B $M R^{2} ω^{2}$
C $\frac{1}{4} M R^{2} ω^{2}$
D $\frac{1}{8} M R^{2} ω^{2}$
Question 2 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed $ω$ . Its rotational kinetic energy is
A $\frac{1}{2} M R^{2} ω^{2}$
B $M R^{2} ω^{2}$
C $\frac{1}{4} M R^{2} ω^{2}$
D $\frac{1}{8} M R^{2} ω^{2}$
Question 3 - Select One
Two discs of moments of inertia $I_{1} and I_{2}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds $ω_{1} and ω_{2}$ are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take $ω_{1} \neq ω_{2}$
ADoes the law of conservation of angular monentum apply to the situation ? Why ?
BFind the angular speed of the two disc system .
CCalculate the loss in kinetic energy of the system in the the process.
DAccount for this loss.

MTG-WBJEE-MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTION-WB-JEE Previous years questions

Home
Ask Doubt
Profile