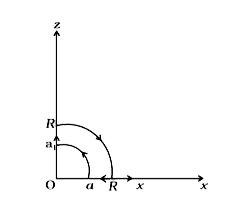
द्विध्रुव आघूर्ण m=mˆk के किसी बिन्दु द्विध्रुव के चुम्बकीय क्षेत्र के लिए ऐम्पियर का नियम सत्यापित कीजिए। C को ऐसा बन्द वक्र मानिए जो दक्षिणावर्त्त गमन करता है (i) z-अक्ष के अनुदिश z=a>0 से z z=R,(ii)x−y तल के प्रथम चतुर्थाश में, केन्द्र मूल बिन्दु पर Rके चौथाई वृत्त के अनुदिश (iii) x-अक्ष के अनुदिश x=R से x=aतक। (iv) x- z तल के प्रथम चतुर्थांश में, केन्द्र मूल बिन्दु पर, a त्रिज्या के चौथाई वृत्त के अनुदिश।
(i) z - अक्ष के अनुदिश
B=μ04p2mr3
R∫aB.dl=μ04π2mR∫adzz3=μ0m2π(−12)(1R2−1a2)
(ii) त्रिज्या R के चौथाई वृत्त के अनुदिश
B∅=μ04π−m.ˆθR3=−μ04πmR3(−sinθ)
B.dl=μ0m4πR2sinθdθ
π2∫0→B.→dl=μ04πR2
(iii) x- अक्ष के अनुदिश
B=μ04π(−mx3)
∫B.d1=0
(iv) त्रिज्या के चौथाई वृत्त के अनुदिश
B.d1=−μ0m4πa2sinθdθ,∫B.d1=−−μ0m4πa2π2∫0sinθdθ=−μ0m4πa2
सभी को जोड़ने पर , ∮CB.d1=0
Topper's Solved these Questions
- चुंबकत्व एवं द्रव्य BOOK - NCERT EXEMPLAR HINDICHAPTER - चुंबकत्व एवं द्रव्य EXERCISE - लघुउत्तरीय (SA)
5 Videos
- गतिमान आवेश और चुम्बकत्व BOOK - NCERT EXEMPLAR HINDICHAPTER - गतिमान आवेश और चुम्बकत्व EXERCISE - दीर्घउत्तरीय (LA)
7 Videos
- तरंग प्रकाशिकी BOOK - NCERT EXEMPLAR HINDICHAPTER - तरंग प्रकाशिकी EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
Similar Questions
R त्रिज्या के गोलाकार के पृष्ठ के लिए मूल बिन्दु पर स्थित m द्विध्रुव आघूर्ण के किसी बिन्दु द्विध्रुव के चुम्बकीय क्षेत्र के लिए गाउस-नियम सत्यापित कीजिए।
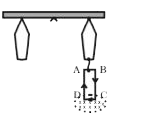
View Solution100 फेरों की कोई आयताकार कुण्डली ABCD (XY तल में) तुला की एक भुजा से लटकी है (चित्र 4.4)। कुण्डली का भार संतुलित करने के लिए दूसरी भुजा पर 500g बाट रखा गया है। अब कुण्डली से 4.9A धारा प्रवाहित की जाती है तथा भीतर की ओर (XZ तल में) कार्यरत 0.2 T का नियत चुम्बकीय क्षेत्र इस प्रकार लगाया जाता है कि केवल CD भुजा जिसकी लम्बाई 1 cm है, कुण्डली क्षेत्र में रहे। तुला पर कितना अतिरिक्त द्रव्यमान .m. रखें कि पुनः संतुलन प्राप्त हो जाए?
View Solution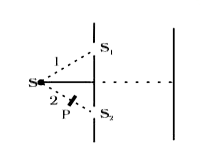
चित्र में एक स्रोत्र जो अध्रुवित प्रकाश उत्सर्जित करता है। द्विझिरी प्रबंध दर्शाया गया है P एक पोलेराइजर जिसके अक्ष की दिशा नहीं दी गई है पोलेराइजर विद्यमान होने पर है यदि मुख्य उच्चिष्ठ की तीव्रताI0 है तब वर्तमान दशा में मुख्य उच्चिष्ठ तथा साथ ही प्रथम निमनिष्ठ की तीव्रता ज्ञात कीजिये।
View Solutionवैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionदो रेखाएं x−31=y+13=z−6−1 तथा x+57=y−2−6=z−34 बिन्दु R पर काटती है । बिन्दु R के XY तल के प्रतिबिम्ब के निर्देशांक है
View Solutionआवेशों के निकाय के कारण विद्युत क्षेत्र || वैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionकिसी बिन्दु-आवेश के कारण तथा आवेशों के निकाय के कारण विद्युत् क्षेत्र
View Solutionबिन्दु द्रव्यमानों के समूह के कारण किसी बिन्दू पर गुरुत्वाकर्षण बल | न्यूटन के गुरुत्वाकर्षण नियम का निगमन (कैप्लर नियम से)
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष तथा केन्द्र पर चुंबकीय क्षेत्र | ऐम्पियर का परिपथीय नियम
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View SolutionBoard Special |विद्युत द्विध्रुव के कारण किसी बिन्दु पर विभव पर आँकिक प्रश्न
View Solutionवैधुत द्विध्रुव|वैधुत द्विध्रुव आघूर्ण|वैधुत द्विध्रुव के कारण अक्षीय स्थिति में वैधुत क्षेत्र|OMR|Summary
View SolutionRecap|वैधुत द्विध्रुव के कारण किसी बिन्दु पर विभव |Question|OMR|Summary
View Solution
