यह मानिए कि पृथ्वी के चुम्बकीय क्षेत्र का द्विध्रुव मॉडल है जिसके अनुसार उस क्षेत्र का अवयव Bv==μ04π2mcosθr3 तथा क्षैतिज अवयव BH=μ04πsinθmr3 तथा θ−90∘- चुम्बकीय विषुवत वृत्त से मापने पर अक्षांश है। उन बिन्दुओं का बिन्दु पथ ज्ञात कीजिए जिनके लिए (i) |B| न्यूनतम है, (ii) नतिकोण शून्य है, (iii) नतिकोण ±45∘ है।
(i) |B|=μ04πmR3(4cos2θ+sin2θ)1/2
|B|2(μ04πR3)2m2=3cos2θ+1,θ=π2 पर न्यूनतम |
|B| चुंबकीय निरक्ष पर न्यूनतम है।
(ii) tan ( नति कोण ) =BVBH=2cotθ
θ=π2 पर नति कोण शून्य हो जाता है। पुनः बिन्दुपथ , चुंबकीय निरक्ष है।
(iii) जब BVBH=1तब नति कोण ±45∘ है।
2cotθ=1
θ=tan−12 बिन्दुपथ है।
Topper's Solved these Questions
- चुंबकत्व एवं द्रव्य BOOK - NCERT EXEMPLAR HINDICHAPTER - चुंबकत्व एवं द्रव्य EXERCISE - लघुउत्तरीय (SA)
5 Videos
- गतिमान आवेश और चुम्बकत्व BOOK - NCERT EXEMPLAR HINDICHAPTER - गतिमान आवेश और चुम्बकत्व EXERCISE - दीर्घउत्तरीय (LA)
7 Videos
- तरंग प्रकाशिकी BOOK - NCERT EXEMPLAR HINDICHAPTER - तरंग प्रकाशिकी EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
Similar Questions
R त्रिज्या के गोलाकार के पृष्ठ के लिए मूल बिन्दु पर स्थित m द्विध्रुव आघूर्ण के किसी बिन्दु द्विध्रुव के चुम्बकीय क्षेत्र के लिए गाउस-नियम सत्यापित कीजिए।
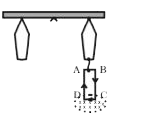
View Solution100 फेरों की कोई आयताकार कुण्डली ABCD (XY तल में) तुला की एक भुजा से लटकी है (चित्र 4.4)। कुण्डली का भार संतुलित करने के लिए दूसरी भुजा पर 500g बाट रखा गया है। अब कुण्डली से 4.9A धारा प्रवाहित की जाती है तथा भीतर की ओर (XZ तल में) कार्यरत 0.2 T का नियत चुम्बकीय क्षेत्र इस प्रकार लगाया जाता है कि केवल CD भुजा जिसकी लम्बाई 1 cm है, कुण्डली क्षेत्र में रहे। तुला पर कितना अतिरिक्त द्रव्यमान .m. रखें कि पुनः संतुलन प्राप्त हो जाए?
View Solution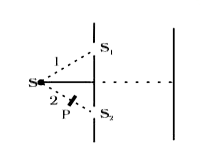
चित्र में एक स्रोत्र जो अध्रुवित प्रकाश उत्सर्जित करता है। द्विझिरी प्रबंध दर्शाया गया है P एक पोलेराइजर जिसके अक्ष की दिशा नहीं दी गई है पोलेराइजर विद्यमान होने पर है यदि मुख्य उच्चिष्ठ की तीव्रताI0 है तब वर्तमान दशा में मुख्य उच्चिष्ठ तथा साथ ही प्रथम निमनिष्ठ की तीव्रता ज्ञात कीजिये।
View Solutionउचित संबंध जोड़िए-
{:(,"स्तम्भ 'अ'",,"स्तम्भ 'ब'"),(1.,"बायो-सेवर्ट का नियम",(a),B=(mu_(0))/(4pi).(2pinI)/r),(2.,"लम्बे ऋजुरेखीय धारावाही चालक के समीप चुम्बकीय क्षेत्र",(b),B=mu_(0)nI),(3.,"धारावाही वृत्तीय कुण्डली के केन्द्र में उत्पन्न चुम्बकीय क्षेत्र",(c),vecF=q(vecvxxvecB)),(4.,"परिनालिका के अक्ष में उत्पन्न चुम्बकीय क्षेत्र",(d),dB=(mu_(0))/(4pi).(Idlsintheta)/(r^(2))),(5.,"लॉरेंज बल",(e),B=(mu_(0))/(4pi).(2I)/d):}
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionयदि xy = 4 तथा x> 0 तो x का वह मान ज्ञात कीजिए जिसके लिए x + y न्यूनतम है।
View Solutionचुंबकीय याम्योत्तर के समांतर ऊर्ध्वाधर तल में घूमने के लिए स्वतंत्र एक चुंबकीय सुई का उत्तरी सिरा क्षैतिज से 60∘ के कोण पर नीचे झुका है। उस स्थान पर पृथ्वी के चुंबकीय क्षेत्र का क्षैतिज घटक 0.4G है। उस स्थान पर पृथ्वी के चुंबकीय क्षेत्र का परिमाण ज्ञात कीजिए।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionउस दीर्घवृत्त का समीकरण जिसका केंद्र मूलबिन्दु है तथा जो बिन्दुओं (-3, 1) तथा (2, -2) से गुजरता है
View Solutionपृथ्वी का चुम्बकीय क्षेत्र तथा अवयव
View Solutionचुम्बकीय द्विध्रुव तथा द्विध्रुव आघूर्ण | परिक्रमण करते इलेक्ट्रान का चुम्बकीय द्विध्रुव आघूर्ण | चुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता
View Solutionएकसमान चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव पर बल आधूर्ण तथा कार्य | पृथ्वी का चुम्बकीय क्षेत्र तथा अवयव | V,H तथा I में सम्बन्ध
View SolutionIf cos2θ−sin2θ−3Cosθ+2=0, 0∘<θ<90∘, then what is the value of 4Cosecθ+Cotθ?
यदि cos2θ−sin2θ−3Cosθ+2=0, है और 0∘<θ<90∘ है, तो 4Cosecθ+Cotθ का मान क्या होगा ?
View Solution
