Given $\to C = \to A \times \to B$ and $\to D = \to B \times \to A$ What is the angle between $\to C$ and $\to D$ ?

A

$30^{\circ}$

B

$60^{\circ}$

C

$90^{\circ}$

D

$180^{\circ}$

Text Solution

Verified by Experts

The correct Answer is:D

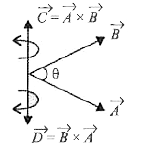
From figure angle between $\to C$ and $\to D$ is $180^{\circ}$

Updated on:21/07/2023

|

Class 12 PHYSICS KINEMATICS

Topper's Solved these Questions

KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks))
10 Videos
KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type (1 Mark) )
9 Videos
KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
1 Videos
HEAT AND THERMAL PHYSICSBOOK - MTG-WBJEECHAPTER - HEAT AND THERMAL PHYSICSEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
15 Videos
KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos

Similar Questions

Knowledge Check

Given $\to C = \to A \times \to B and \to D = \to B \times \to A$ . What is the angle between $\to C$ and $\to D$ ?
A $30^{\circ}$
B $60^{\circ}$
C $90^{\circ}$
D $180^{\circ}$
If $\to a, \to b, \to c, \to d$ are unit vectors such that $\to a . \to b = \frac{1}{2}$ , $\to c . \to d = \frac{1}{2}$ and angle between $\to a \times \to b$ and $\to c \times \to d$ is $\frac{π}{6}$ then the value of $∣ ∣ [\to a \to b \to d] \to c - [\to a \to b \to c] \to d ∣ ∣ =$
A $3 / 2$
B $3 / 4$
C $3 / 8$
D2

MTG-WBJEE-KINEMATICS -WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type (2 Marks))

Home
Ask Doubt
Profile