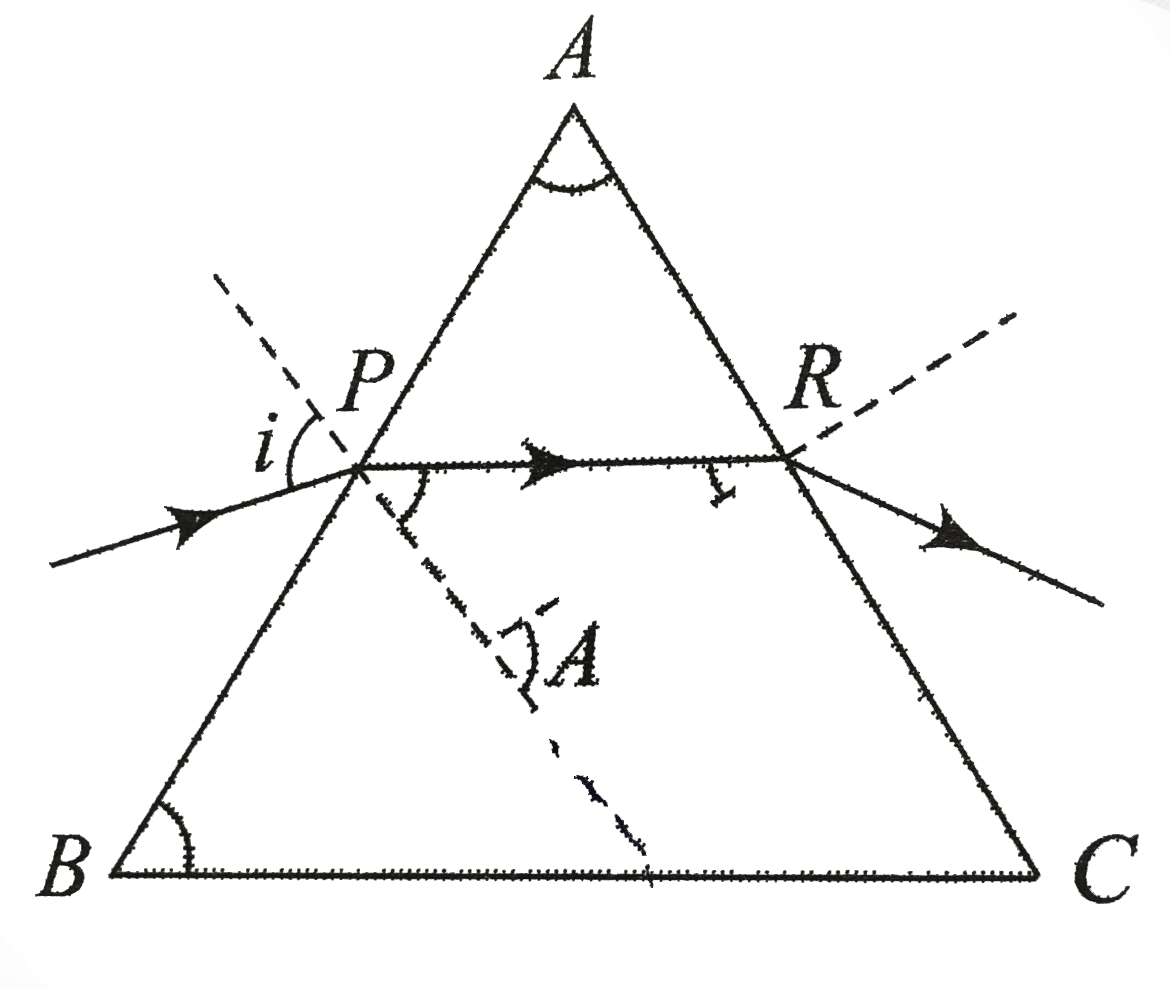
A ray of light undergoes deviation of $30^{\circ}$ when incident on the equilateral prism of refractive index $\sqrt{2}$ . What is the angle subtended by the ray inside the prism with the base of the prism?

Text Solution

Verified by Experts

Here $δ = 30^{\circ} and A = 60^{\circ}$
So if the prism had been in minimum deviation,
$μ = \frac{sin [30^{\circ} + 60^{\circ}] / 2}{sin (60^{\circ} / 2)} = \frac{{sin 45}^{\circ}}{{sin 30}^{\circ} =} \frac{1}{\sqrt{2}} \times 2 = \sqrt{2}$
And as $μ$ of the prism is given to be $\sqrt{2}$

The prism is in the position implies that
$r_{1} = r_{2} = r = (\frac{A}{2}) = (\frac{60^{\circ}}{2}) = 30^{\circ}$
Therefore, angle subtended by the ray inside the prism with the surface $A B (90^{\circ} - r) = (90^{\circ} - 30^{\circ}) = 60^{\circ}$ and as base also subtends an angle of $60^{\circ}$ with the face AB, the ray inside the prism in parallel to the base i.e., the angle subtended by the ray inside the prism with the base is zero.

Updated on:21/07/2023

A ray of light undergoes deviation of $30^{\circ}$ when incident on an equilateral prism of refractive index $\sqrt{2}$ . The angle made by the ray inside the prism with the base of the prism is
A $15^{\circ}$
B $0^{\circ}$
C $45^{\circ}$
D $30^{\circ}$
A ray of light suffers minimum deviation when incident on an equilateral prism of refractive index $\sqrt{2}$ . What is the angle of incidence ?
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$