A converging lens forms a real image 1 of an object on its principle axis. A rectangular slab of refractive index μ and thickness x is introduced between I and the lens, Imagw I will move
towards the lens by (μ−1)x
away from the lens by (1−1μ)x
away from the lens (μ−1)x
towards the lens by (1−1μ)x
The correct Answer is:B
Topper's Solved these Questions
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE II
113 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
Similar Questions
A converging lens forms a real image I on its optic axis. A rectangular galss slab of refractive index μ and thickness t is introduced between the lens and I. I will move
View SolutionP is a point on the axis of a concave mirror. The image of P, formed by the mirror, coincides with P. A rectangular glass slab of thickness t and refractive index μ is now introduced between P and the mirror. For the image of P to coincide with P again, the mirror must be moved
View Solution
Knowledge Check
A converging lens forms a real image I on its optic axis. A rectangular galss slab of refractive index μ and thickness t is introduced between the lens and I. I will move
Aaway from the lens by (μ−1)Btowards the lens by t(μ−1)Caway from the lens by t(μ−1μ)Dtowards the lens by t(μ−1μ)A convex lens form a real image of a point object placed on its principal axis. If the upper half of the lens is painted black, the image will
ABe shifted downwardsBBe shifted upwardsCNot be shiftedDShift on the principal axisP is a point on the axis of a concave mirror. The image of P, formed by the mirror, coincides with P. A rectangular glass slab of thickness t and refractive index μ is now introduced between P and the mirror. For the image of P to coincide with P again, the mirror must be moved
Atowards P by (μ−1)tBaway from P by (μ−1)tCaway from P by t(1−1μ)Dtowards P by t(1−1μ)
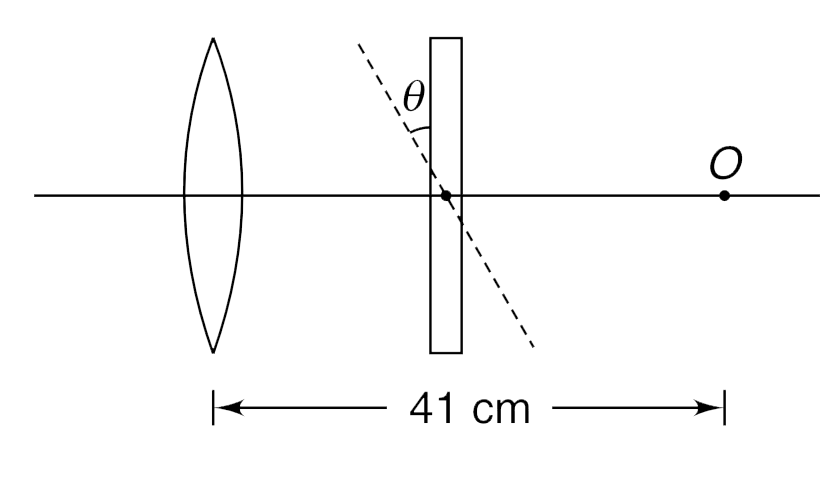
A point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
View SolutionA biconvex lens of focal length 40 cm is placed in front of an object at a distance of 20 cm . Now a slab of refractive index 43 is placed somewhere in between the lens and the object. The shift in the image formed after the introduction of slab equals (thickness of the slab is 2 mm)
View SolutionA lens is made of three thin different mediums. Radius of curvature and refractive index of each medium is shown iin Figure., Surface AB is straight. An object is placed at some distance from the lens by which a real image is formed on the screen placed at a distance of 10cm from the lens. Find

a. The distance of the object from the lens.
b. A slab of thiskness 1.5cm and refractive index 1.5 is introduced between the image and the lens. Find the new position of the object so that image is again formed on the screen.
c. Find the position of the image when same slabe is placed on the other side of the lens {as in part (b)}
View SolutionA biconvex lens forms a real image of an object placed perpendicular to its principal axis. Suppose the radii of curvature of the lens tend to infinity. Then the image would
View SolutionA biconvex lens of focal length 40 cm is placed in front of an object at a distance of 20 cm . Now a slab of refractive index 43 is placed somewhere in between the lens and the object. The shift in the image formed after the introduction of slab equals (thickness of the slab is 2 mm)
View Solution
