The velocity of a particle of mass 1 kg is given by v=10√x the work done by the forceacting on the particle during its motion from x=4 to x=9m is
250J
300J
350J
400J
The correct Answer is:A
To solve the problem, we need to determine the work done by the force acting on a particle as it moves from x=4 m to x=9 m. The velocity of the particle is given by the equation v=10√x.
1. Identify the given parameters:
- Mass of the particle, m=1 kg
- Velocity, v=10√x
2. Calculate acceleration:
- We know that acceleration a can be expressed as:
a=vdvdx
- First, we need to differentiate the velocity with respect to x:
v=10√x⟹dvdx=10⋅12√x=5√x
- Now, substituting v and dvdx into the acceleration formula:
a=10√x⋅5√x=50 m/s2
3. Calculate the force:
- Using Newton's second law, F=ma:
F=1 kg⋅50 m/s2=50 N
4. Calculate the displacement:
- The displacement d when moving from x=4 m to x=9 m is:
d=xf−xi=9 m−4 m=5 m
5. Calculate the work done:
- Work done W is given by the formula:
W=F⋅d
- Substituting the values we found:
W=50 N⋅5 m=250 J
Final Answer:
The work done by the force acting on the particle during its motion from x=4 m to x=9 m is 250 Joules.
---
- Mass of the particle, m=1 kg
- Velocity, v=10√x
- We know that acceleration a can be expressed as:
a=vdvdx
- First, we need to differentiate the velocity with respect to x:
v=10√x⟹dvdx=10⋅12√x=5√x
- Now, substituting v and dvdx into the acceleration formula:
a=10√x⋅5√x=50 m/s2
- Using Newton's second law, F=ma:
F=1 kg⋅50 m/s2=50 N
- The displacement d when moving from x=4 m to x=9 m is:
d=xf−xi=9 m−4 m=5 m
- Work done W is given by the formula:
W=F⋅d
- Substituting the values we found:
W=50 N⋅5 m=250 J
The work done by the force acting on the particle during its motion from x=4 m to x=9 m is 250 Joules.
Topper's Solved these Questions
Similar Questions
The velocity (v) of a pariticle of mass m moving along x-axls is given by v=b√x, where b is a constant. Find work done by the force acting on the particle during its motion from x=0 to x=4m.
View SolutionThe velocity (v) of a particle of mass m moving along x-axis is given by v=α√x, where α is a constant. Find work done by force acting on particle during its motion from x=0 to x=2m :-
View Solution
Knowledge Check
A particle moves along the X - axis with velocity v=k√x . What will be work done by the forces acting on particle during interval it moves from x = 0 to x = d ? (Assume mass of the aprticle is m ) .
A12mk2dB14mk2dC12mkd2D14mkd2A force F is related to the position of a particle by the relation F=(10x2)N. The work done by the force when the particle moves from x= 2 m to x = 4 m is
A563JB560JC5603JD3560JThe velocity - time graph of a particle of mass 10 kg is shown in the figure. The net work done on the particle in the first two seconds of the motion is
 A−9300JB12000JC−4500JD−12000J
A−9300JB12000JC−4500JD−12000J
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
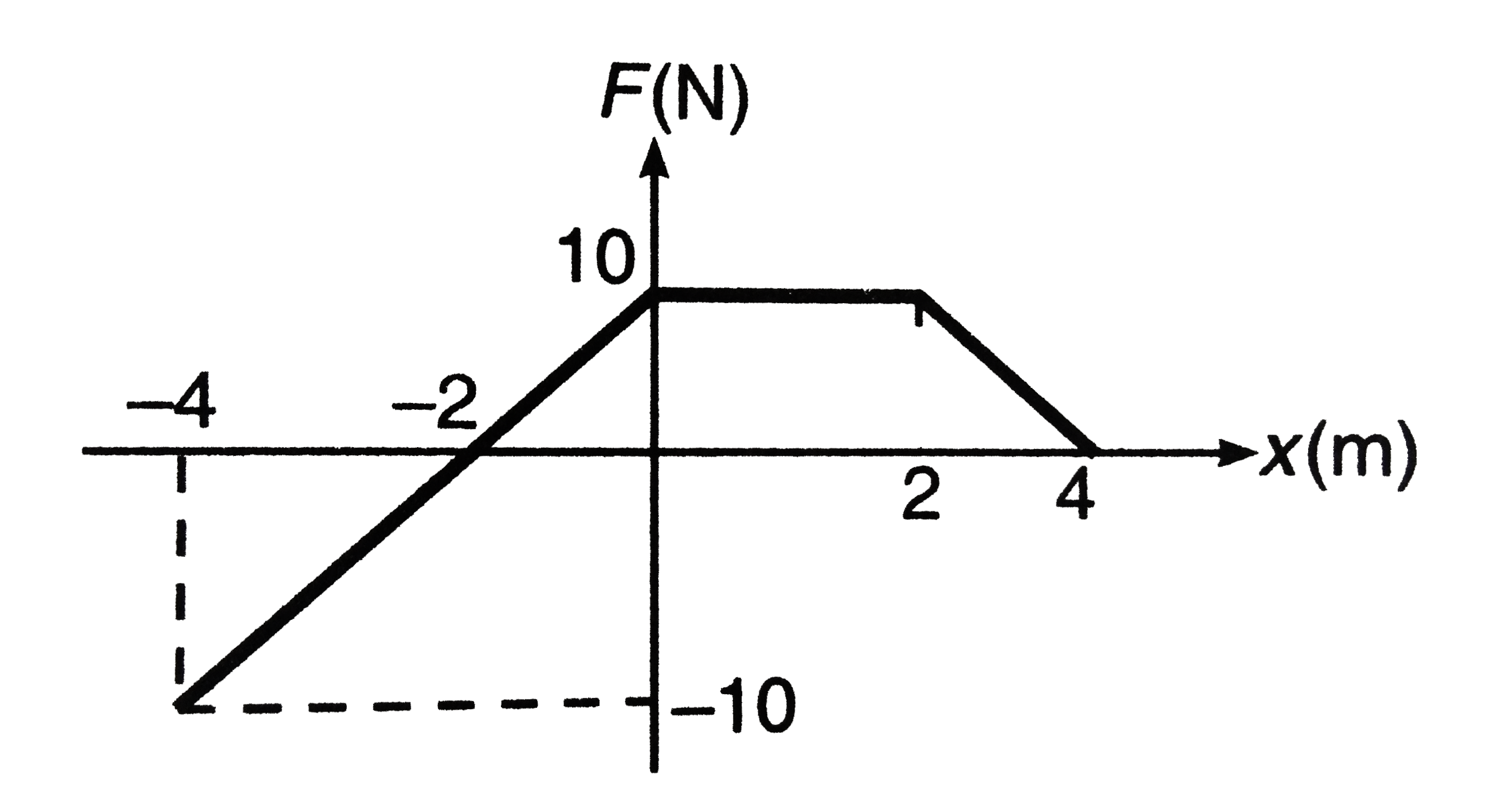 .
.
View SolutionForce acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionIn the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3ˆi+4ˆj)m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :
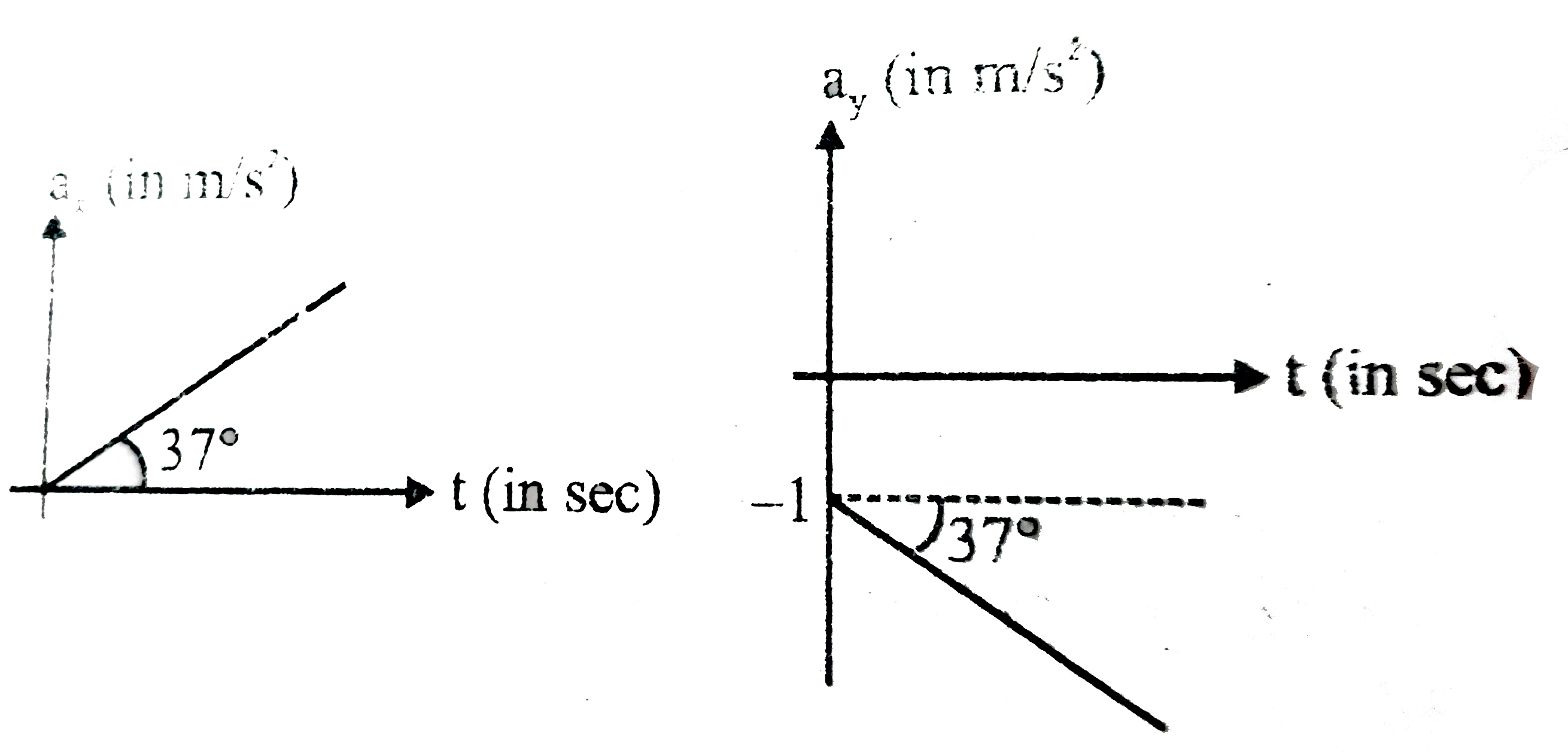
View SolutionA particle of mass m moves with a variable velocity v, which changes with distance covered x along a straight line as v=k√x, where k is a positive constant. The work done by all the forces acting on the particle, during the first t seconds is
View Solution
