The total force acting on the mass at any time t, for damped oscillator is given as (where symbols have their usual meanings)
→F=−k→x
→F=−k→x−b→v
→F=−k→x−b→v+2→x
→F=−b→v−bk2→x
The correct Answer is:B
To solve the problem regarding the total force acting on a mass in a damped oscillator, we need to analyze the forces involved. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Forces Acting on the Mass
In a damped oscillator, there are two primary forces acting on the mass:
1. Spring Force (Restoring Force): This force is proportional to the displacement from the equilibrium position and acts in the opposite direction of the displacement. It can be expressed as:
Fspring=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
2. Damping Force: This force opposes the motion of the mass and is proportional to the velocity of the mass. It can be expressed as:
Fdamping=−bv
where b is the damping coefficient and v is the velocity of the mass.
Step 2: Write the Total Force Equation
The total force Ftotal acting on the mass is the sum of the spring force and the damping force. Therefore, we can write:
Ftotal=Fspring+Fdamping
Substituting the expressions for the forces, we get:
Ftotal=−kx−bv
Step 3: Final Expression for Total Force
Thus, the total force acting on the mass at any time t can be expressed as:
Ftotal=−kx−bdxdt
where dxdt represents the velocity v.
Conclusion
The total force acting on the mass in a damped oscillator is given by:
Ftotal=−kx−bv
In a damped oscillator, there are two primary forces acting on the mass:
1. Spring Force (Restoring Force): This force is proportional to the displacement from the equilibrium position and acts in the opposite direction of the displacement. It can be expressed as:
Fspring=−kx
where k is the spring constant and x is the displacement from the equilibrium position.
Fdamping=−bv
where b is the damping coefficient and v is the velocity of the mass.
The total force Ftotal acting on the mass is the sum of the spring force and the damping force. Therefore, we can write:
Ftotal=Fspring+Fdamping
Substituting the expressions for the forces, we get:
Ftotal=−kx−bv
Thus, the total force acting on the mass at any time t can be expressed as:
Ftotal=−kx−bdxdt
where dxdt represents the velocity v.
The total force acting on the mass in a damped oscillator is given by:
Ftotal=−kx−bv
Topper's Solved these Questions
Similar Questions
Knowledge Check
Bohr magnetonis given by (symbols have their usual meanings)
A4πmeeh2B4πmeehCeh24πmeDeh4πmeThe correct combination is (symbols have their usual meanings)
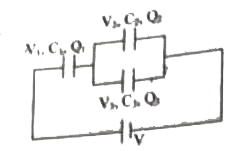 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3Select the incorrect relation. (Where symboles have their usual meanings):-
ACp=γRγ−1BCP−CV=RCΔU=PfVf−PiVi1−γDCv=Rγ−1
Mechanically work done is equal to (symbols have their usual meanings)
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View SolutionThe correct form of Stroke's law is (symbols have their usual meanings)
View SolutionChoose the correct arrangement, where the symbols have their usual meanings
View SolutionThe average intensity of electromagnetic wave is (where symbols have their usual meanings)
View Solution
