A sphere made of transparent material of refractive index (μ=32 )and of radius 50 cm has a small air bubble 10 cm below the surface. The apparent depth of the bubble if viewed from outside normally is
507 cm
257cm
1007 cm
757cm
The correct Answer is:A
To find the apparent depth of the air bubble in the sphere made of transparent material, we can use the formula for refraction at a spherical surface. The formula we will use is derived from the lens maker's formula and is given by:
μ2v−μ1u=μ2−μ1R
Where:
- μ1 is the refractive index of the medium from which the light is coming (in this case, air, so μ1=1).
- μ2 is the refractive index of the medium in which the object is located (the sphere, so μ2=32).
- u is the object distance (the distance of the bubble from the surface of the sphere, which is −10 cm since it's below the surface).
- v is the image distance (the apparent depth we want to find).
- R is the radius of curvature of the sphere (which is −50 cm, as it is negative for a spherical surface).
1. Identify the values:
- μ1=1 (for air)
- μ2=32 (for the sphere)
- u=−10 cm (the bubble is below the surface)
- R=−50 cm (the radius of the sphere)
2. Substitute the values into the formula:
32v−1−10=32−1−50
3. Simplify the right side:
32−1−50=12−50=−1100
4. Rewrite the equation:
32v+110=−1100
5. Find a common denominator for the left side:
32v+10100=−1100
6. Combine the fractions:
32v=−1100−10100=−11100
7. Cross-multiply to solve for v:
32=−11v100
3⋅100=−11v⋅2
300=−22v
v=−30022=−15011 cm
8. Calculate the apparent depth:
The negative sign indicates that the image is virtual and located inside the sphere. The apparent depth is given by the absolute value:
Apparent Depth=15011 cm≈13.64 cm
Final Answer:
The apparent depth of the bubble when viewed from outside is approximately 13.64 cm.
- μ1 is the refractive index of the medium from which the light is coming (in this case, air, so μ1=1).
- μ2 is the refractive index of the medium in which the object is located (the sphere, so μ2=32).
- u is the object distance (the distance of the bubble from the surface of the sphere, which is −10 cm since it's below the surface).
- v is the image distance (the apparent depth we want to find).
- R is the radius of curvature of the sphere (which is −50 cm, as it is negative for a spherical surface).
- μ1=1 (for air)
- μ2=32 (for the sphere)
- u=−10 cm (the bubble is below the surface)
- R=−50 cm (the radius of the sphere)
32v−1−10=32−1−50
32−1−50=12−50=−1100
32v+110=−1100
32v+10100=−1100
32v=−1100−10100=−11100
32=−11v100
3⋅100=−11v⋅2
300=−22v
v=−30022=−15011 cm
The negative sign indicates that the image is virtual and located inside the sphere. The apparent depth is given by the absolute value:
Apparent Depth=15011 cm≈13.64 cm
The apparent depth of the bubble when viewed from outside is approximately 13.64 cm.
Topper's Solved these Questions
Similar Questions
A hollow sphere made of a transparent material of refractive index 1.5 has a small mark on its surface as shown. The mark is observed from the farther side. Find the distance of the image of mark from the centre of the sphere.

View Solution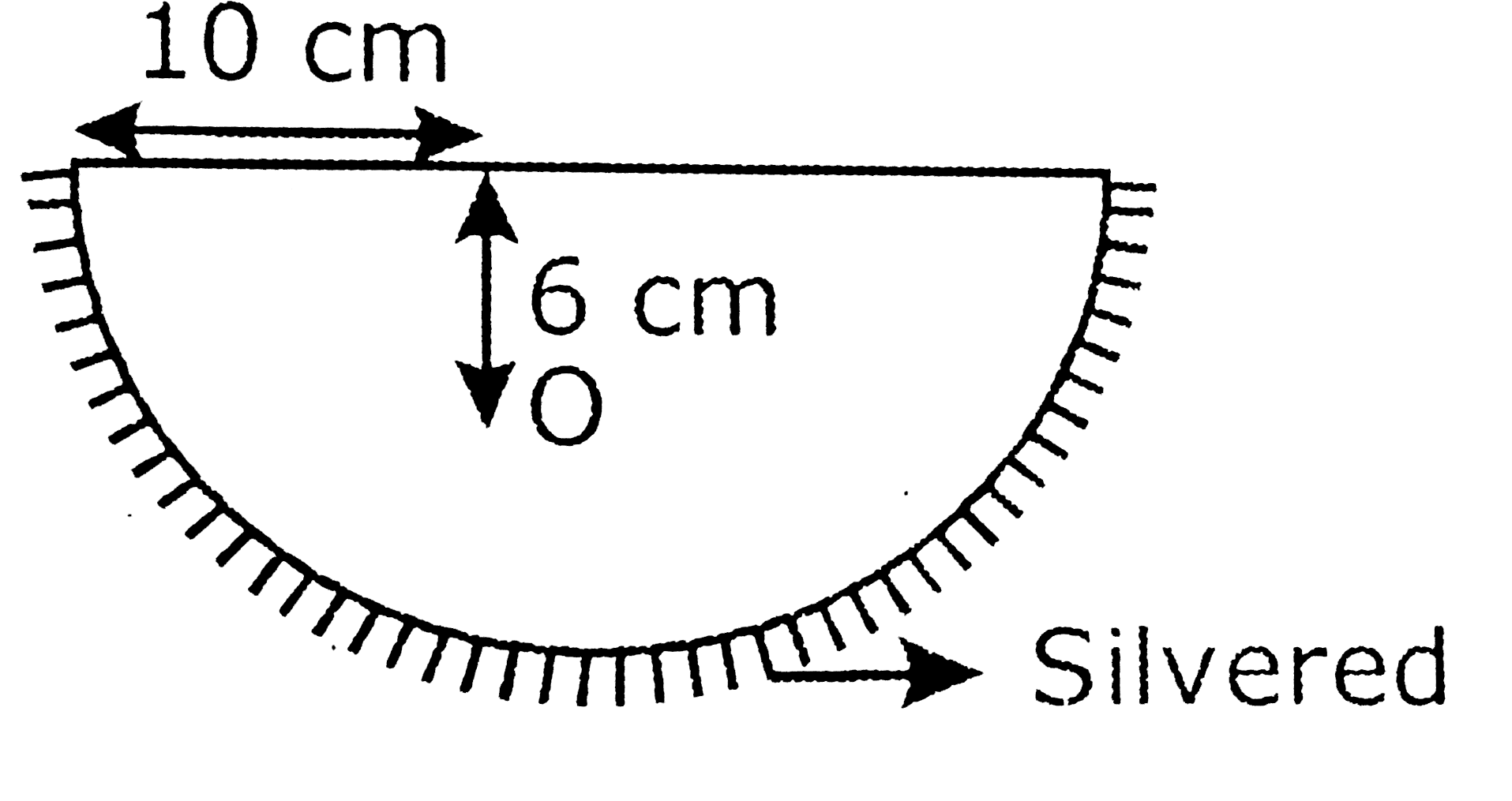
A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface . A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
View Solution
Knowledge Check
A glass sphere (μ =1.5) of radius 20 cm has small air bubble 4 cm below its centre. The sphere is viewed from outside and along vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
A13.33B26.67C15D30A small air bubble of radius 0.1 mm is situated at a depth of 10 m below the free surface of water .The external pressure on the bubble will be
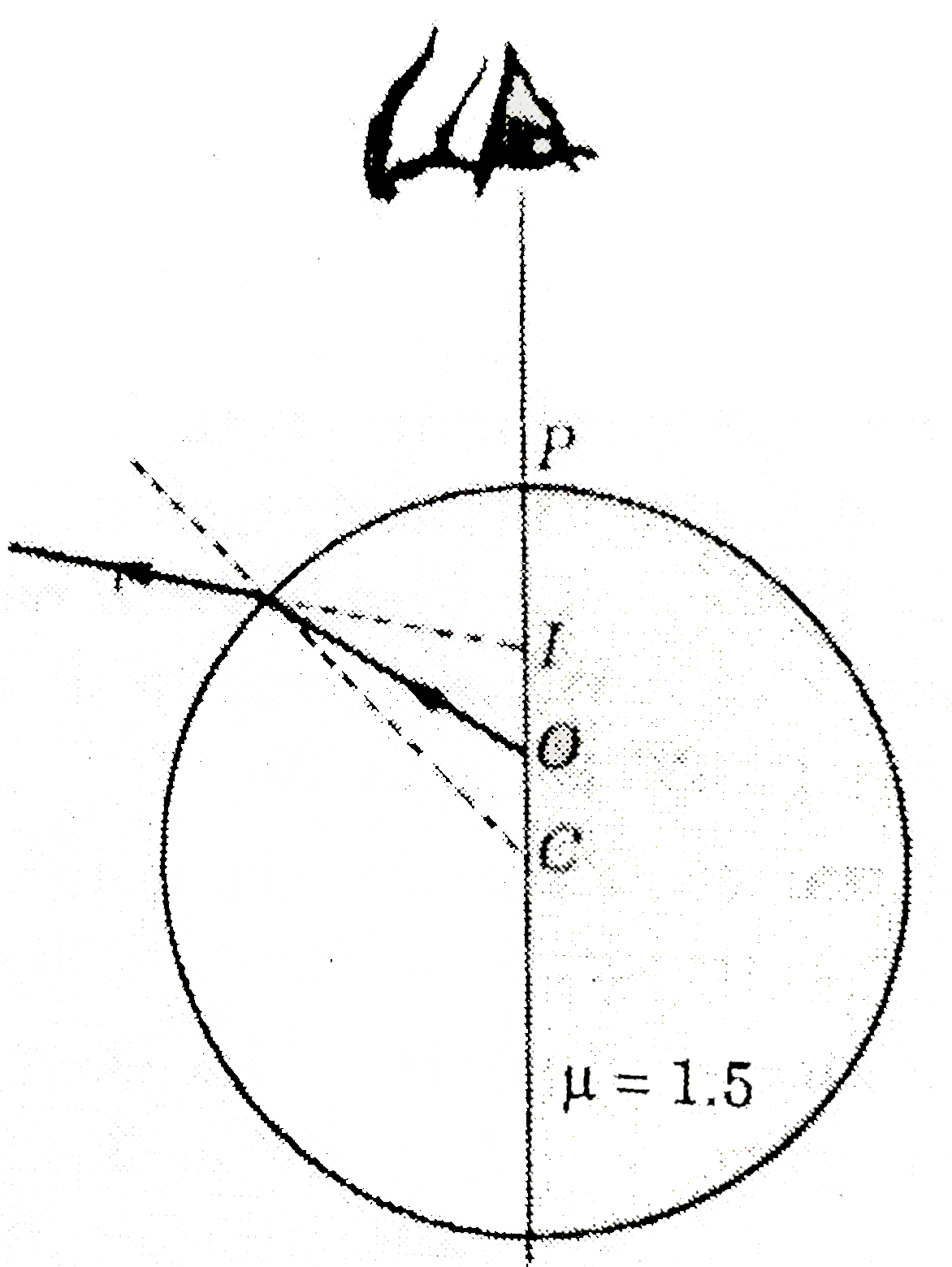
A0.5×105N/m2B105N/m2C2×105N/m2D4×105N/m2Fig shows a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. the bubble is 4.0 cm below the surface and is viewed normally from the outside. Find the apparent depth of the bubble.
 A2cmB3cmC4cmD5cm
A2cmB3cmC4cmD5cm
Fig shows a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. the bubble is 4.0 cm below the surface and is viewed normally from the outside. Find the apparent depth of the bubble.

View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionA spherical solid glass paper weight of diameter 6 cm has a small air bubble at a distance of 1.5 cm from the centre. If the air bubble be viewed from the side to which it is nearest along the line joining the bubble and the centre, find where will it appear.
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionA pond of depth 20 cm is filled with water of refractive index 4/3. Calculate apparent depth of the tank when viewed normally.
View Solution
