The average value of cos2(ϕ2) in one cycle is
Zero
13
12
14
The correct Answer is:C
To find the average value of cos2(ϕ/2) over one complete cycle (from 0 to 2π), we can follow these steps:
Step 1: Set up the average value formula
The average value ⟨f⟩ of a function f(ϕ) over the interval from a to b is given by:
⟨f⟩=1b−a∫baf(ϕ)dϕ
In this case, a=0, b=2π, and f(ϕ)=cos2(ϕ/2).
Step 2: Write the integral for the average value
Substituting the values into the formula, we get:
⟨cos2(ϕ/2)⟩=12π∫2π0cos2(ϕ/2)dϕ
Step 3: Use the trigonometric identity
To simplify cos2(ϕ/2), we can use the identity:
cos2(x)=1+cos(2x)2
Applying this to our function:
cos2(ϕ/2)=1+cos(ϕ)2
Step 4: Substitute the identity into the integral
Now we substitute this into our integral:
⟨cos2(ϕ/2)⟩=12π∫2π01+cos(ϕ)2dϕ
This simplifies to:
⟨cos2(ϕ/2)⟩=14π∫2π0(1+cos(ϕ))dϕ
Step 5: Evaluate the integral
Now we can evaluate the integral:
∫2π0(1+cos(ϕ))dϕ=∫2π01dϕ+∫2π0cos(ϕ)dϕ
The first integral is:
∫2π01dϕ=2π
The second integral is:
∫2π0cos(ϕ)dϕ=0
Thus:
∫2π0(1+cos(ϕ))dϕ=2π+0=2π
Step 6: Substitute back into the average value formula
Now substituting back into the average value formula:
⟨cos2(ϕ/2)⟩=14π⋅2π=12
Final Result
The average value of cos2(ϕ/2) in one cycle is:
12
The average value ⟨f⟩ of a function f(ϕ) over the interval from a to b is given by:
⟨f⟩=1b−a∫baf(ϕ)dϕ
In this case, a=0, b=2π, and f(ϕ)=cos2(ϕ/2).
Substituting the values into the formula, we get:
⟨cos2(ϕ/2)⟩=12π∫2π0cos2(ϕ/2)dϕ
To simplify cos2(ϕ/2), we can use the identity:
cos2(x)=1+cos(2x)2
Applying this to our function:
cos2(ϕ/2)=1+cos(ϕ)2
Now we substitute this into our integral:
⟨cos2(ϕ/2)⟩=12π∫2π01+cos(ϕ)2dϕ
This simplifies to:
⟨cos2(ϕ/2)⟩=14π∫2π0(1+cos(ϕ))dϕ
Now we can evaluate the integral:
∫2π0(1+cos(ϕ))dϕ=∫2π01dϕ+∫2π0cos(ϕ)dϕ
The first integral is:
∫2π01dϕ=2π
The second integral is:
∫2π0cos(ϕ)dϕ=0
Thus:
∫2π0(1+cos(ϕ))dϕ=2π+0=2π
Now substituting back into the average value formula:
⟨cos2(ϕ/2)⟩=14π⋅2π=12
The average value of cos2(ϕ/2) in one cycle is:
12
Topper's Solved these Questions
Similar Questions
Knowledge Check
The maximum values of the phasors (currents and voltage) in AC circuits can be treated as vectors rotating with an angular frequency equal to the angular frequency of the rotor of the generator. If the phase difference between two phasors −→A1 and −→A2 is ϕ the resultant phasor is :
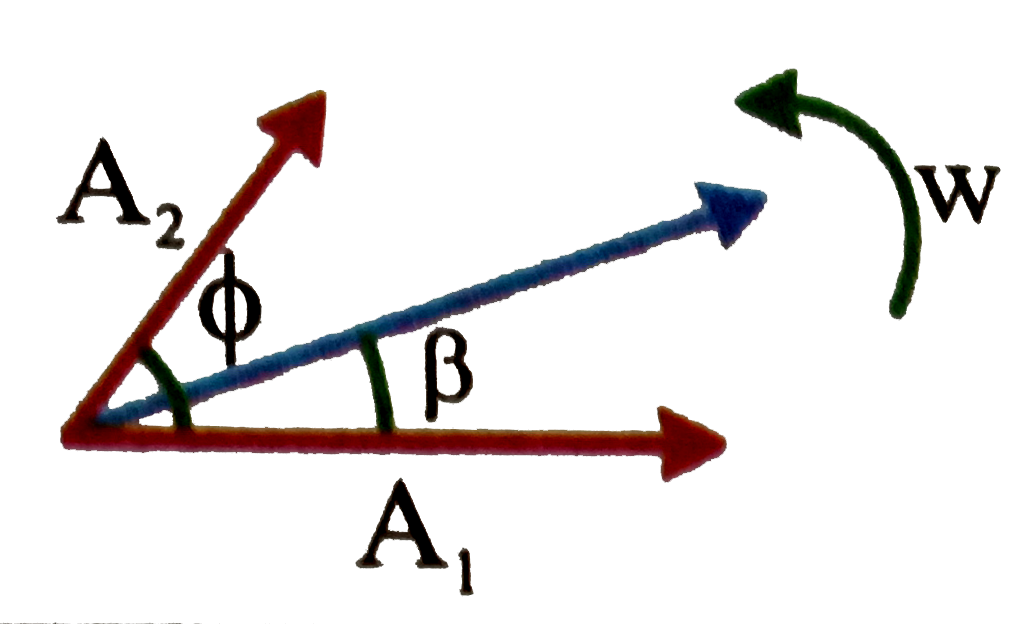
A=√A21+A22+2A1A2cosϕ
and the phase of →A with respects to A1 is
β=tan−1A2sinϕA1+A2cosϕ
RHS value
The rms value of y=f(t) is
yrms=⎧⎨⎩∫T0[f(t)]2dtT⎫⎬⎭12
Average value
The average value of y=f(t) is yav=∫T0ydtT
Using the above concept, answer the following questions.
The average value of i in i−t graph (Semi circular) is
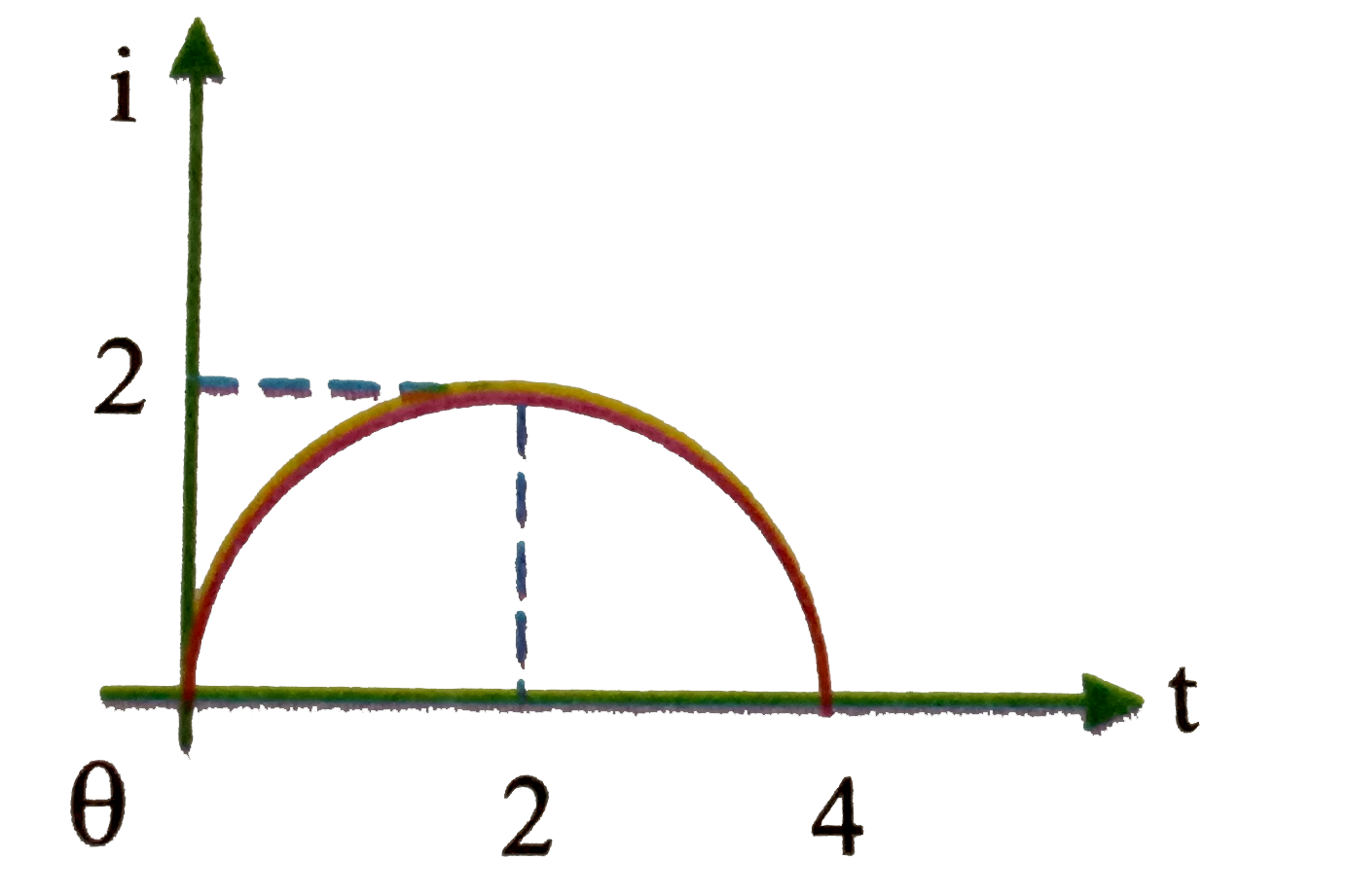 AπBπ2Cπ3Dπ√2
AπBπ2Cπ3Dπ√2The values of cos2(θ−ϕ)2−sin2(θ+ϕ)2 is
AcosθBcosϕCcosθcosϕDNone of theseThe value of cos2(θ−ϕ)2−sin2(θ+ϕ)2 is
AcosθBcosϕCcosθcosϕDNone of these
If 3(cot2ϕ−cos2ϕ)=cos2ϕ,0∘<ϕ<90∘, then the value of (tan2ϕ+cosec2ϕ+sin2ϕ) is:
View SolutionIf sinθ+sinϕ=a,cosθ+cosϕ=b, find the value of sin(θ+ϕ) and cos2θ+cos2ϕ where |b|>|a|
View SolutionAverage value of alternating current for one positive half cycle is ………. Of the peak value .
View SolutionIf a=cosθ+isinθ,b=cosϕ+isinϕ,find the values of cos(θ+ϕ) and cos(θ−ϕ) in terms of a and b.
View SolutionThe value of tan2ϕ+cot2ϕ−sec2ϕcosec2ϕ is equal to:
View Solution
