In mu-particle scattering experiment, the expression of distance of closest approach (r0)is (symbols have their usual meanings)
14πε0×Ze2E
14πε0×2Ze2E
14πε0×(Z2e2)
14πε0×Z2e4E
The correct Answer is:B
To solve the problem regarding the distance of closest approach (r0) in a mu-particle scattering experiment, we can derive the expression step by step.
Step 1: Understand the Concept
The distance of closest approach refers to the minimum distance between the incoming particle (in this case, a muon) and the target nucleus during a scattering event. This distance can be derived from the principles of electrostatics and conservation of energy.
Step 2: Use the Relevant Formula
For a charged particle (like a muon) approaching a nucleus, the distance of closest approach can be derived from the balance of kinetic energy and potential energy. The potential energy at the distance of closest approach is given by Coulomb's law:
U=k⋅Z⋅e2r0
where:
- U is the potential energy,
- k is Coulomb's constant,
- Z is the atomic number of the nucleus,
- e is the charge of the muon,
- r0 is the distance of closest approach.
Step 3: Set Up the Energy Conservation Equation
The kinetic energy of the muon before the interaction is given by:
K.E.=12mv2
where:
- m is the mass of the muon,
- v is the velocity of the muon.
At the distance of closest approach, all the kinetic energy is converted into potential energy:
12mv2=k⋅Z⋅e2r0
Step 4: Rearranging the Equation
Rearranging the above equation to solve for r0:
r0=2k⋅Z⋅e2mv2
Step 5: Final Expression
Thus, the expression for the distance of closest approach r0 in a mu-particle scattering experiment is:
r0=2k⋅Z⋅e2mv2
The distance of closest approach refers to the minimum distance between the incoming particle (in this case, a muon) and the target nucleus during a scattering event. This distance can be derived from the principles of electrostatics and conservation of energy.
For a charged particle (like a muon) approaching a nucleus, the distance of closest approach can be derived from the balance of kinetic energy and potential energy. The potential energy at the distance of closest approach is given by Coulomb's law:
- U is the potential energy,
- k is Coulomb's constant,
- Z is the atomic number of the nucleus,
- e is the charge of the muon,
- r0 is the distance of closest approach.
The kinetic energy of the muon before the interaction is given by:
- m is the mass of the muon,
- v is the velocity of the muon.
Rearranging the above equation to solve for r0:
Thus, the expression for the distance of closest approach r0 in a mu-particle scattering experiment is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
The correct combination is (symbols have their usual meanings)
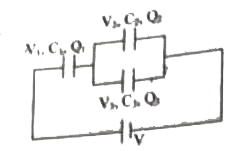 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3The correct form of Stroke's law is (symbols have their usual meanings)
A→F=−6πηa→vB→F=6πηa→vC→F=−4πηa→vD→F=4πηa→vBohr magnetonis given by (symbols have their usual meanings)
A4πmeeh2B4πmeehCeh24πmeDeh4πme
Mechanically work done is equal to (symbols have their usual meanings)
View SolutionMechanically work done is equal to (symbols have their usual meanings)
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View SolutionChoose the correct arrangement. The symbols have their usual meanings
View SolutionThe average intensity of electromagnetic wave is (where symbols have their usual meanings)
View Solution
